题目内容
【题目】如图①，在△ABC中，∠ACB=90°，BC=2，∠A=30°，点E，F分别是线段BC，AC的中点，连接EF．
（1）说明线段BE与AF的位置关系和数量关系；
（2）如图②，当△CEF绕点C顺时针旋转α（0°＜α＜90°）时，连接AF，BE，（1）中的结论是否仍然成立？如果成立，请证明；如果不成立，请说明理由；
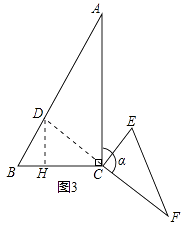
（3）如图③，当△CEF绕点C顺时针旋转α（0°＜α＜180°）时，延长FC交AB于点D，如果AD=6﹣2 
，求旋转角α的度数．
【答案】
（1）
解：BE⊥AF，AF= 
BE；理由如下：
∵在△ABC中，∠ABC=90°，BC=2，∠A=30°，
∴AC= BC=2 ，
∵点E，F分别是线段BC，AC的中点，
∴BE⊥AF，BE=CE，AF=CF，
∴ 
= ，
∴AF= BE
（2）
解：（1）中的结论仍然成立，理由如下：
∵点E，F分别是线段BC，AC的中点，
∴EC= 
BC，FC= AC，
∴ 
= ，
∵∠BCE=∠ACF=α，
∴△BEC∽△AFC，
∴ = ，∠CBE=∠CAF，
延长BE交AC于点O，交AF于点M，如图2所示：
∵∠BOC=∠AOM，∠CBE=∠CAF，
∴∠BCO=∠AMO=90°，
∴BE⊥AF
（3）
解：∵∠ACB=90°，BC=2，∠A=30°，
∴AB=2BC=4，∠B=60°，
∴DB=AB﹣AD=4﹣（6﹣2 ）=2 ﹣2，
过点D作DH⊥BC于点H，如图3所示：
∴BH= DB= ﹣1，DH= 
DB=3﹣ ，
又∵CH=BC﹣BH=2﹣（ ﹣1）=3﹣ ，
∴CH=DH，
∴∠HCD=45°，
∴∠DCA=45°，
∴α=180°﹣45°=135°．
【解析】（1）由含30°角的直角三角形的性质得出AC= BC=2 ，由已知得出BE⊥AF，BE=CE，AF=CF，得出 
= ，即可得出结论；（2）由中点的定义得出EC= BC，FC= AC，得出 = ，再由∠BCE=∠ACF=α，证出△BEC∽△AFC，得出 = ，∠CBE=∠CAF，延长BE交AC于点O，交AF于点M，如图2所示：由三角形内角和定理证出∠BCO=∠AMO=90°，得出BE⊥AF；（3）由直角三角形的性质得出AB=2BC=4，∠B=60°，得出DB=AB﹣AD=2 ﹣2，过点D作DH⊥BC于点H，由直角三角形的性质得出BH= DB= ﹣1，DH= DB=3﹣ ，求出CH=3﹣ ，得出CH=DH，由等腰直角三角形的性质得出∠HCD=45°，得出∠DCA=45°，求出α=135°即可．
【考点精析】通过灵活运用旋转的性质，掌握①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了即可以解答此题．
