题目内容
【题目】抛物线y=ax2+bx+c（a≠0）上部分点的横坐标x，纵坐标y的对应值如表：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 0 | 4 | 6 | 6 | 4 | 0 | … |
（1）求这个二次函数的表达式；
（2）直接写出当y＜0时x的取值范围．
【答案】
（1）解：设抛物线的表达式为：y=a（x+2）（x﹣3），
把（0，6）代入得：6=﹣6a，
a=﹣1，
∴抛物线的表达式为：y=﹣（x+2）（x﹣3）=﹣x2+x+6
（2）解：如图所示，由图象得：当y＜0时，x的取值范围是：x＜﹣2或x＞3．
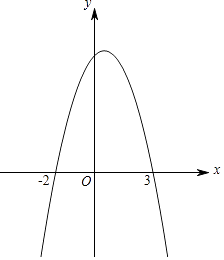
【解析】（1）根据待定系数法求二次函数的表达式；（2）画图象，根据图象直角写出当y＜0时x的取值范围．
【考点精析】本题主要考查了抛物线与坐标轴的交点的相关知识点，需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．才能正确解答此题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】我市某中学举办“网络安全知识答题竞赛”，初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩如图所示．
平均分（分） | 中位数（分） | 众数（分） | 方差（分2） | |
初中部 | a | 85 | b | s初中2 |
高中部 | 85 | c | 100 | 160 |
（1）根据图示计算出a、b、c的值；
（2）结合两队成绩的平均数和中位数进行分析，哪个队的决赛成绩较好？
（3）计算初中代表队决赛成绩的方差s初中2，并判断哪一个代表队选手成绩较为稳定．
