题目内容
【题目】阅读材料:我们都知道,![]()
于是,-2x2+40x+5
=-2(x2-20x)+5
=-2(x2-20x+100)+200+5
=-2(x-10)2+205
又因为![]() ,所以
,所以![]() ,
,![]()
所以,-2x2+40x+5有最大值205.
如图,某农户准备用长34米的铁栅栏围成一边靠墙的长方形羊圈ABCD和一个边长为1米的正方形狗屋CEFG.设AB=x米.
(1)请用含x的代数式表示BC的长(直接写答案);
(2)设山羊活动范围即图中阴影部分的面积为S,试用含x的代数式表示S,并计算当x=5时S的值;
(3)试求出山羊活动范围面积S的最大值.
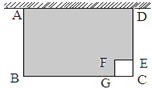
【答案】(1)BC=32-2x;(2)S=-2x2+32x-1,当x=5时,S=109米2;(3)山羊活动范围ABGFE面积S的最大值是127平方米.
【解析】
(1)依题意得AB=DC=x,EF=FG=1,根据铁栅栏总长为34米即可用x表示出BC的长;
(2)根据S=S长方形ABCD-S正方形CEFG列出S与x的函数关系式,进而求出当x=5时S的值;
(3)配方后根据完全平方式恒小于等于0,即可求出最大值以及x的值即可.
(1)依题意得AB=DC=x,EF=FG=1,
∵AB+DC+BC+EF+FG=34,
∴2x+BC+2=34,
∴BC=32-2x;
(2)依题意得S=S长方形ABCD-S正方形CEFG=x(32-2x)-1=-2x2+32x-1,
当x=5时,S=-2×52+32×5-1=109(米2);
(3)S=-2x2+32x-1=-2(x2-16x+64)+127=-2(x-8)2+127,
又因为-2<0,
所以,(x-8)2≥0,-2(x-8)2≤0,-2(x-8)2+127≤127,
所以,山羊活动范围ABGFE面积S的最大值是127平方米.

 阅读快车系列答案
阅读快车系列答案【题目】如图所示,为厉行节能减排,倡导绿色出行,某公司拟在我市甲、乙两个街道社区投放一批共享单车(俗称“小黄车”),这批自行车包括A、B两种不同款型.
成本单价 (单位:元) | 投放数量 (单位:辆) | 总价(单位:元) | |
A型 | x | 50 | 50x |
B型 | x+10 | 50 |
|
成本合计(单位:元) | 7500 | ||
问题1:看表填空
如图2所示,本次试点投放的A、B型“小黄车”共有 辆;用含有x的式子表示出B型自行车的成本总价为 ;
问题2:自行车单价
试求A、B两型自行车的单价各是多少?
问题3:投放数量
现在该公司采取如下方式投放A型“小黄车”:甲街区每100人投放n辆,乙街区每100人投放(n+2)辆,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有![]() 人,求甲街区每100人投放A型“小黄车”的数量.
人,求甲街区每100人投放A型“小黄车”的数量.