题目内容
【题目】证明:如果两个三角形中有两条边和其中一边上的中线对应相等,那么这两个三角形全等.(写出已知,求证,画出图形并证明)
【答案】见解析
【解析】
根据题意构造两个三角形,用SSS定理证明△ABD≌△A1B1D1,得到∠B=∠B1.再用边角边定理证明△ABC≌△A1B1C1.
已知:△ABC,△A1B1C1 中,AB=A1B1,BC=B1C1,AD,A1D1 分别为 BC,B1C1
边上的中线,AD=A1D1.
求证:△ABC≌△A1B1C1.
证明:∵AD,A1D1 分别为 BC,B1C1 边上的中线,
∴BD=![]() BC,B1D1=
BC,B1D1=![]() B1C1,
B1C1,
又∵BC=B1C1,
∴BD=B1D1,
在△ABD 和△A1B1D1 中,
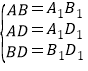 ,
,
∴△ABD≌△A1B1D1(SSS),
∴∠B=∠B1,
∵在△ABC 与△A1B1C1 中,
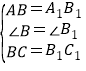 ,
,
∴△ABC≌△A1B1C1(SAS).

练习册系列答案
相关题目