题目内容
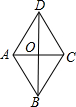 如图所示,在菱形ABCD中,AC、BD相交于O,且AC:BD=1:
如图所示,在菱形ABCD中,AC、BD相交于O,且AC:BD=1:| 3 |
分析:首先设AO=x,由在菱形ABCD中,AC:BD=1:
,AB=2,可得方程AB2=(
x)2+x2=22;继而可求得AC与BD的长,则可求得菱形ABCD的面积.
| 3 |
| 3 |
解答:解:菱形两对角线将其分割为四个全等的直角三角形.
设AO=x,
∵四边形ABCD为菱形,
∴AO=CO,BO=DO,AC⊥BD.
又∵AC:BD=1:
,
∴AO:BO=1:
,BO=
x.
在Rt△ABO中,
∵AB2=BO2+AO2,
∴AB2=(
x)2+x2=22.
解得:x=1.
∴AO=1,BO=
.
∴AC=2,BD=2
.
∴菱形的面积为:
×2×2
=2
.
设AO=x,
∵四边形ABCD为菱形,
∴AO=CO,BO=DO,AC⊥BD.
又∵AC:BD=1:
| 3 |
∴AO:BO=1:
| 3 |
| 3 |
在Rt△ABO中,
∵AB2=BO2+AO2,
∴AB2=(
| 3 |
解得:x=1.
∴AO=1,BO=
| 3 |
∴AC=2,BD=2
| 3 |
∴菱形的面积为:
| 1 |
| 2 |
| 3 |
| 3 |
点评:此题考查了菱形的性质以及勾股定理.此题难度不大,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
相关题目
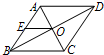 7、如图所示,在菱形ABCD中,AC、BD相交于点O,E为AB中点,若OE=3,则菱形ABCD的周长是( )
7、如图所示,在菱形ABCD中,AC、BD相交于点O,E为AB中点,若OE=3,则菱形ABCD的周长是( )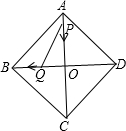 如图所示,在菱形ABCD中,AC,BD交于点O,AB=15,AO=12,P从A出发,Q从O出发,分别以2cm/s和1cm/s的速度各自向O,B点运动,当运动时间为多少秒时,四边形BQPA的面积是△POQ面积的8倍.
如图所示,在菱形ABCD中,AC,BD交于点O,AB=15,AO=12,P从A出发,Q从O出发,分别以2cm/s和1cm/s的速度各自向O,B点运动,当运动时间为多少秒时,四边形BQPA的面积是△POQ面积的8倍.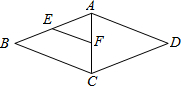 (2012•保定二模)如图所示,在菱形ABCD中,点E,F分别为AB,AC的中点,菱形ABCD的周长为32,则EF的长等于( )
(2012•保定二模)如图所示,在菱形ABCD中,点E,F分别为AB,AC的中点,菱形ABCD的周长为32,则EF的长等于( ) 如图所示,在菱形ABCD中,AB=AC=3cm,求∠BCD的大小和菱形的周长.
如图所示,在菱形ABCD中,AB=AC=3cm,求∠BCD的大小和菱形的周长.