Question

【题目】在甲乙两个不透明的口袋中，分别有大小、材质完全相同的小球，其中甲口袋中的小球上分别标有数字1，2，3，乙口袋中的小球上分别标有数字2，3，4，先从甲袋中任意摸出一个小球，记下数字为m，再从乙袋中摸出一个小球，记下数字为n．

（1）请用列表或画树状图的方法表示出所有(m，n)可能的结果；

（2）小明和小利做游戏，若m，n都是方程x2﹣5x+6=0的解时，则小明获胜；若m，n都不是方程x2﹣5x+6=0的解时，则小利获胜，这个游戏对双方公平吗？为什么？

Answer 1

【答案】（1）结果为：(1，2)，(1，3)，(1，4)，(2，2)，(2，3)，(2，4)，(3，2)，(3，3)，(3，4)；（2）这个游戏对双方不公平．理由见解析．

【解析】

（1）根据画树形图即可表示出所有可能出现的结果；
（2）分别求出两个人赢的概率，再进行判断即可．

（1）利用树状图表示为：

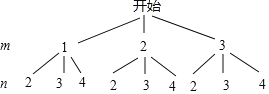
（2）这个游戏对双方不公平．理由如下：

因为m，n都是方程x2﹣5x+6=0的解，

所以m=2，n=3，或m=3，n=2．

由树状图可知：共有9个等可能的结果，

m、n都是方程x2﹣5x+6=0的解的结果有2个，

m，n都不是方程x2﹣5x+6=0的解的结果有1个，

两个都不是解时 m=1，n=4

所以小明获胜的概率为，小利获胜的概率为，

所以两个人获胜的概率不一样大．

答：游戏对双方不公平．