题目内容
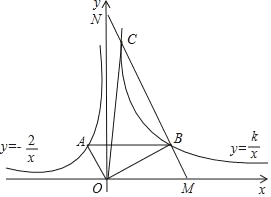
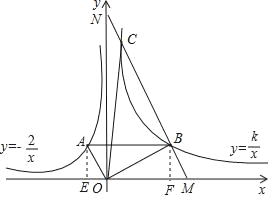
【题目】如图,∠AOB=90°,反比例函数y=﹣![]() (x<0)的图象过点A(﹣1,a),反比例函数y=
(x<0)的图象过点A(﹣1,a),反比例函数y=![]() (k>0,x>0)的图象过点B,且AB∥x轴.
(k>0,x>0)的图象过点B,且AB∥x轴.
(1)求a和k的值;
(2)过点B作MN∥OA,交x轴于点M,交y轴于点N,交双曲线y=![]() 于另一点C,求△OBC的面积.
于另一点C,求△OBC的面积.
【答案】(1)a=2,k=8(2)![]() =15.
=15.
【解析】分析:(1)把A(-1,a)代入反比例函数![]() 得到A(-1,2),过A作AE⊥x轴于E,BF⊥x轴于F,根据相似三角形的性质得到B(4,2),于是得到k=4×2=8;
得到A(-1,2),过A作AE⊥x轴于E,BF⊥x轴于F,根据相似三角形的性质得到B(4,2),于是得到k=4×2=8;
(2)求的直线AO的解析式为y=-2x,设直线MN的解析式为y=-2x+b,得到直线MN的解析式为y=-2x+10,解方程组得到C(1,8),于是得到结论.
详解:(1)∵反比例函数y=﹣![]() (x<0)的图象过点A(﹣1,a),
(x<0)的图象过点A(﹣1,a),
∴a=﹣![]() =2,
=2,
∴A(﹣1,2),
过A作AE⊥x轴于E,BF⊥⊥x轴于F,
∴AE=2,OE=1,
∵AB∥x轴,
∴BF=2,
∵∠AOB=90°,
∴∠EAO+∠AOE=∠AOE+∠BOF=90°,
∴∠EAO=∠BOF,
∴△AEO∽△OFB,
∴![]() ,
,
∴OF=4,
∴B(4,2),
∴k=4×2=8;
(2)∵直线OA过A(﹣1,2),
∴直线AO的解析式为y=﹣2x,
∵MN∥OA,
∴设直线MN的解析式为y=﹣2x+b,
∴2=﹣2×4+b,
∴b=10,
∴直线MN的解析式为y=﹣2x+10,
∵直线MN交x轴于点M,交y轴于点N,
∴M(5,0),N(0,10),
解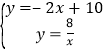 得,
得,![]() ,
,
∴C(1,8),
∴△OBC的面积=S△OMN﹣S△OCN﹣S△OBM=![]() 5×10﹣
5×10﹣![]() ×10×1﹣
×10×1﹣![]() ×5×2=15.
×5×2=15.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目