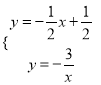题目内容
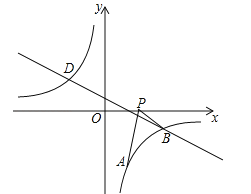
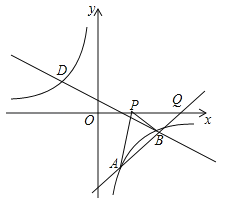
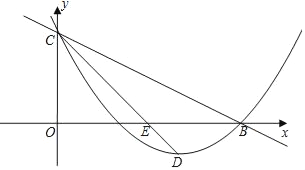
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2﹣2x+c与直线y=﹣![]() x+3分别交于x轴、y轴上的B、C两点,抛物线的顶点为点D,联结CD交x轴于点E.
x+3分别交于x轴、y轴上的B、C两点,抛物线的顶点为点D,联结CD交x轴于点E.
(1)求抛物线的解析式以及点D的坐标;
(2)求tan∠BCD;
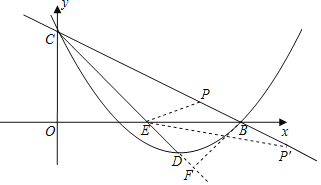
(3)点P在直线BC上,若∠PEB=∠BCD,求点P的坐标.
【答案】(1)D(4,﹣1);(2)![]() ;(3)点P(
;(3)点P(![]() ,
,![]() )或(12,﹣3).
)或(12,﹣3).
【解析】分析:(1)直接利用待定系数法求出二次函数解析式进而得出答案;
(2)利用锐角三角函数关系得出EC,BF的长,进而得出答案;
(3)分别利用①点P在x轴上方,②点P在x轴下方,分别得出点P的坐标.
详解:(1)由题意得B(6,0),C(0,3),
把B(6,0)C(0,3)代入y=ax2-2x+c
得![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为:y=![]() x2-2x+3
x2-2x+3
=![]() (x2-8x)+3
(x2-8x)+3
=![]() (x-4)2-1,
(x-4)2-1,
∴D(4,-1);
(2)可得点E(3,0),
OE=OC=3,∠OEC=45°,
过点B作BF⊥CD,垂足为点F
在Rt△OEC中,EC=![]() ,
,
在Rt△BEF中,BF=BEsin∠BEF=![]() ,
,
同理,EF=![]() ,
,
∴CF=![]() +
+![]() =
=![]() ,
,
在Rt△CBF中,tan∠BCD=![]() ;
;
(3)设点P(m,![]() m+3)
m+3)
∵∠PEB=∠BCD,
∴tan∠PEB=tan∠BCD=![]() ,
,
①点P在x轴上方
∴![]() ,
,
解得:m=![]() ,
,
∴点P(![]() ,
,![]() ),
),
②点P在x轴下方
∴![]() ,
,
解得:m=12,
∴点P(12,-3),
综上所述,点P(![]() ,
,![]() )或(12,-3).
)或(12,-3).

练习册系列答案
相关题目