Question

【题目】在平面直角坐标系中，已知抛物线与轴交于点和点（点在点的左侧），与轴交于点，对称轴是直线．

（1）求抛物线的表达式；

（2）直线平行于轴，与抛物线交于、两点（点在点的左侧），且，点关于直线的对称点为，求线段的长；

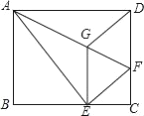
（3）点是该抛物线上一点，且在第一象限内，联结、，交线段于点，当时，求点的坐标．

Answer 1

【答案】（1）y=-x2+2x+3；（2）；（3）（，）或（，)．

【解析】

（1）根据抛物线与轴交于点可得出c的值，然后由对称轴是直线可得出b的值，从而可求出抛物线的解析式；
（2）令y=0得出关于x的一元二次方程，求出x，可得出点A、B的坐标，从而得到AB的长，再求出MN的长，根据抛物线的对称性求出点M的横坐标，再代入抛物线解析式求出点M的纵坐标，再根据点的对称可求出OE的长；
（3）过点E作x轴的平行线EH，分别过点F，P作EH的垂线，垂足分别为G，Q，则FG∥PQ，先证明△EGF∽△EQP，可得，设点F的坐标为（a，-a+3），则EG=a，FG=-a+3-=-a+，可用含a的式子表示P点的坐标，根据P在抛物线的图象上，可得关于a的方程，把a的值代入P点坐标，可得答案．

解：（1）将点C（0，3）代入得c=3，

又抛物线的对称轴为直线x=1，

∴-=1，解得b=2，

∴抛物线的表达式为y=-x2+2x+3；

（2）如图，

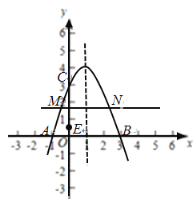
令y=0，则-x2+2x+3=0，解得x1=-1，x2=3，
∴点A（-1，0），B（3，0），∴AB=3-（-1）=4，
∵，∴MN=×4=3，
根据二次函数的对称性，点M的横坐标为，

代入二次函数表达式得，y=，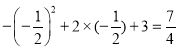

∴点M的坐标为，

又点C的坐标为（0，3），点C与点E关于直线MN对称，

∴CE=2×（3-）=，

∴OE=OC-CE=；

（3）如图，过点E作x轴的平行线EH，分别过点F，P作EH的垂线，垂足分别为G，Q，则FG∥PQ，

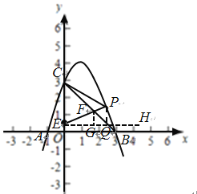
设直线BC的解析式为y=kx+b（k≠0），

则，解得，

∴直线BC的解析式为y=-x+3，

设点F的坐标为（a，-a+3），则EG=a，FG=-a+3-=-a+．

∵FG∥PQ，∴△EGF∽△EQP，

∴．

∵，∴FP:EF=1:2，∴EF:EP=2:3．

∴，

∴EQ=EG=a，PQ=FG=（-a+）=-a+，

∴xP=a，yP=-a++=-a+，即点P的坐标为（a，-a+），

又点P在抛物线y=-x2+2x+3上，

∴-a+=-a2+3a+3，化简得9a2-18a+5=0，

解得a=或a=，符合题意，

∴点P的坐标为（，）或（，)．