题目内容
【题目】如图,□ABCD中,BD=2AD , AC交BD于点O , E为OA的中点,M为DC的中点,观察EM与DC的数量关系,并说明你的理由.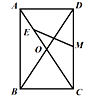
【答案】解:EM=![]() DC
DC
理由:如图:连结 DE.
∵ 四边形ABCD是平行四边形.
∴BD=2OD.
又∵BD=2AD,
∴ AD=OD,
∴ △ADO 为等腰三角形.
又 ∵E为AO 的中点.
∴DE![]() AO.
AO.
△DEC 为直角三角形, CD为斜边.
又 ∵M 为斜边CD 的中点.
∴EM=![]() CD.
CD.
【解析】如图:连结 DE.由平行四边形的性质得BD=2OD.由BD=2AD,得 AD=OD,△ADO为等腰三角形.由其性质得DE![]() AO.由直角三角形中
AO.由直角三角形中
斜边上的中线等于斜边的一半即可。
【考点精析】根据题目的已知条件,利用直角三角形斜边上的中线和平行四边形的性质的相关知识可以得到问题的答案,需要掌握直角三角形斜边上的中线等于斜边的一半;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目