Question

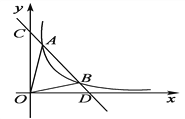
【题目】如图，在平面直角坐标系xOy中，直线y＝2x＋n与x轴、y轴分别交于点A，B，与双曲线y＝在第一象限内交于点C(1，m)．

(1)求m和n的值；

(2)过x轴上的点D(3，0)作平行于y轴的直线l，分别与直线AB和双曲线y＝交于点P，Q，求△APQ的面积．

Answer 1

【答案】（1）2（2）

【解析】

试题（1）先把C（1，m）代入y=可求出m，确定C点坐标，然后把C点坐标代入直线y=2x+n可求得n的值；

（2）先利用直线y=2x+2，令x=0和3，分别确定A点和P点坐标；再通过y=，令x=3，确定Q点坐标，然后利用三角形面积公式计算即可．

试题解析：（1）把C（1，m）代入y=中得m=，解得m=4，

∴C点坐标为（1，4），

把C（1，4）代入y=2x+n得4=2×1+n，解得n=2；

（2）∵对于y=2x+2，令x=3，则y=2×3+2=8，

得到P点坐标为（3，8）；

令y=0，则2x+2=0，则x=-1，

得到A点坐标为（-1，0），

对于y=，令x=3，则y=，

得到Q点坐标为（3，），

∴△APQ的面积=ADPQ=×（3+1）×（8-）=．