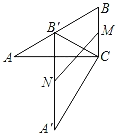
题目内容
【题目】已知抛物线![]()
(1)求证:抛物线与![]() 轴总有两个不同的交点.
轴总有两个不同的交点.
(2)设抛物线与![]() 轴的交点为点
轴的交点为点![]() 和点
和点![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
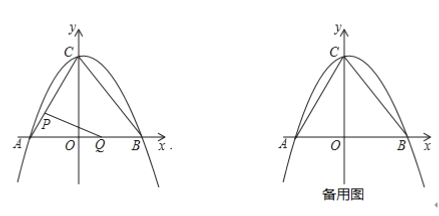
①若![]() 为直角三角形且
为直角三角形且![]() ,点
,点![]() 在直线
在直线![]() 上方的抛物线上,且
上方的抛物线上,且![]() 是锐角,求
是锐角,求![]() 的取值范围.
的取值范围.
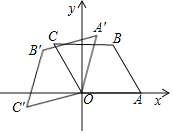
②设抛物线顶点为![]() ,在抛物线上是否存在一点
,在抛物线上是否存在一点![]() ,使以点
,使以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为平行四边形?若存在请求出
为顶点的四边形为平行四边形?若存在请求出![]() 的值;若不存在请说明理由.
的值;若不存在请说明理由.
【答案】(1)证明见解析;(2)①![]() ,②存在,
,②存在,![]() 或
或![]() .
.
【解析】
(1)令![]() ,再根据根的判别式求解即可.
,再根据根的判别式求解即可.
(2)①分别求出A、B、C的坐标,再根据勾股定理求得![]() ,联立方程求出点E的坐标,根据图象求出
,联立方程求出点E的坐标,根据图象求出![]() 的取值范围.②根据抛物线解析式可得,对称轴为
的取值范围.②根据抛物线解析式可得,对称轴为![]() ,设
,设![]() ,根据
,根据![]() ,可得当
,可得当![]() 即
即![]() 时,以点D、O、C为顶点才能构成等腰三角形,当
时,以点D、O、C为顶点才能构成等腰三角形,当![]() 时,分三种情况进行讨论即可.
时,分三种情况进行讨论即可.
(1)当![]() 时,
时,![]()
∵![]()
∴抛物线与x轴总有两个不同的交点.
(2)①当![]() 时,
时,![]()
![]()
∴![]()
∵A在B的左侧且![]()
∴![]()
当![]() 时,
时,![]()
∴![]()
∵![]()
∴![]()
即![]()
解得![]()
∴![]()
联立得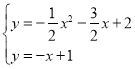
解得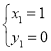 或
或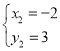
如图
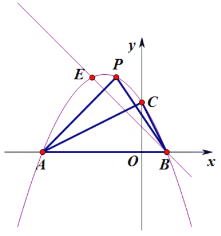
∴![]() 与抛物线的另一个交点
与抛物线的另一个交点![]()
∵P在直线![]() 上方的抛物线上,且
上方的抛物线上,且![]() 是锐角
是锐角
∴![]() .
.
②存在
∵![]()
∴对称轴为![]()
设![]()
∵![]()
∴当![]() 即
即![]() 时,以点D、O、C为顶点才能构成等腰三角形
时,以点D、O、C为顶点才能构成等腰三角形
当![]() 时,分三种情况
时,分三种情况
1)若![]() ,则
,则![]() ,即
,即![]()
解得![]()
∴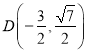 或
或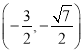
2)若![]() ,则
,则![]() ,即
,即![]()
解得![]()
∴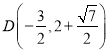 或
或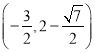
3)若![]() ,则
,则![]()
综上所述,在抛物线对称轴上存在一点D,使以点DOC为顶点成等腰三角形,此时![]() .
.

【题目】某商店出售一款商品,商店规定该商品的销售单价不低于68元,经市场调查反映,该商品的日销售量y(件)与销售单价x(元)之间满足一次函数关系,关于该商品的销售单价,日销售量,日销售利润的部分对应数据如下表:[注:日销售利润=日销售量×(销售单价-成本单价)]
销售单价x(元) | 75 | 78 | 82 |
日销售量y(件) | 150 | 120 | 80 |
日销售利润w(元) | 5250 | 4560 | m |
(1)求y关于x的函数关系式,并直接写出自变量的取值范围;
(2)根据以上信息,
①填空:该产品的成本单价是_______元,表中m的值是______;
②求w关于x的函数关系式;
(3)求该商品日销售利润的最大值.