题目内容
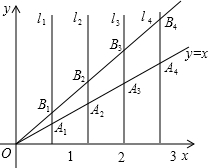 (2012•峨边县模拟)如图,直线l1、l2、l3…ln同垂直于x轴,垂足依次为(1,0)(2,0)(3,0)(4,0)…(n,0)函数y=x分别相交于A1、A2、A3…A;函数y=2x分别与直线 l1、l2、l3…ln相交于B1、B2、B3…Bn,如果△A1OB1的面积为S1,四边形A1A2B2B1的面积记为S2,四边形A2A3B3B2的面积记为S3…,四边形An-1AnBnBn-1的面积记为Sn,那么S1=
(2012•峨边县模拟)如图,直线l1、l2、l3…ln同垂直于x轴,垂足依次为(1,0)(2,0)(3,0)(4,0)…(n,0)函数y=x分别相交于A1、A2、A3…A;函数y=2x分别与直线 l1、l2、l3…ln相交于B1、B2、B3…Bn,如果△A1OB1的面积为S1,四边形A1A2B2B1的面积记为S2,四边形A2A3B3B2的面积记为S3…,四边形An-1AnBnBn-1的面积记为Sn,那么S1=| 1 |
| 2 |
| 1 |
| 2 |
50
50
.分析:由A1的坐标可以求出B1的坐标,从而可以求出A1B1的长度,A1B1边上的高是1就可以求出S1的值,根据A1、A2…An在y=x上,由垂足就可以求出A1、A2…An的坐标,由B1、B2…Bn在y=2x的图象上,可以求出B1、B2…Bn的坐标,就可以求出A1B1、A2B2…AnBn的值就可以求出S2、S3…Sn的值,这样就可以求出S1+S2+S3+…+S10的值.
解答:解:∵l1、l2、l3…ln同垂直于x轴,垂足依次为(1,0)(2,0)(3,0)(4,0)…(n,0)且与函数y=x分别相交于A1、A2、A3…An,
∴A1、A2、A3…An,的坐标分别为:(1,1)(2,2)(3,3)(4,4)…(n,n).
∵l1、l2、l3…ln与y=2x分别相交于B1、B2、B3…Bn,
∴B1、B2、B3…Bn的坐标分别为:(1,2)(2,4)(3,6)(4,8)…(n,2n).
∴A1B1、A2B2…AnBn的值分别为1,2,3,…n.
∴S1=
=
,
S2=
=
,
S3=
=
,
S4=
=
,
…
Sn=
∴S1+S2+S3+…+S10=
+
+
+…+
=50.
故答案为:
,50.
∴A1、A2、A3…An,的坐标分别为:(1,1)(2,2)(3,3)(4,4)…(n,n).
∵l1、l2、l3…ln与y=2x分别相交于B1、B2、B3…Bn,
∴B1、B2、B3…Bn的坐标分别为:(1,2)(2,4)(3,6)(4,8)…(n,2n).
∴A1B1、A2B2…AnBn的值分别为1,2,3,…n.
∴S1=
| 1×1 |
| 2 |
| 1 |
| 2 |
S2=
| (1+2)×1 |
| 2 |
| 3 |
| 2 |
S3=
| (2+3)×1 |
| 2 |
| 5 |
| 2 |
S4=
| (3+4)×1 |
| 2 |
| 7 |
| 2 |
…
Sn=
| 2n-1 |
| 2 |
∴S1+S2+S3+…+S10=
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 19 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题是一道一次函数的综合试题,考查了垂直于x轴上的点的坐标的特征,三角形和梯形的面积公式的运用.在解答中找到这些图形的高都为1是关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目

 (2012•峨边县模拟)如图,A(1,-3),B(4,-1),P(a,0),N(a+2,0),当四边形ABNP的周长最小时,a=
(2012•峨边县模拟)如图,A(1,-3),B(4,-1),P(a,0),N(a+2,0),当四边形ABNP的周长最小时,a= (2012•峨边县模拟)如图,AD∥BC,∠A=90°,BC=BD,CE⊥BD.
(2012•峨边县模拟)如图,AD∥BC,∠A=90°,BC=BD,CE⊥BD.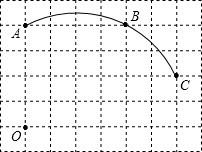 (2012•峨边县模拟)如图在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
(2012•峨边县模拟)如图在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.