Question

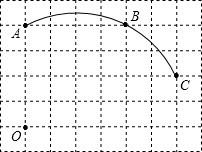（2012•峨边县模拟）如图在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C．
（1）请完成如下操作：
①以点O为坐标原点、竖直和水平方向为轴、网格边长为单位长，建立平面直角坐标系； ②根据图形提供的信息，标出该圆弧所在圆的圆心D，并连接AD、CD．
（2）请在（1）的基础上，完成下列填空：
①写出点的坐标：C

（6，2）

、D

（2，0）

；
②⊙D的半径=

2

5

（结果保留根号）；
③若E（7，0），试判断直线EC与⊙D的位置关系，并说明你的理由．

Answer 1

分析：（1）根据题意建立平面直角坐标系，然后作出弦AB的垂直平分线，以及BC的垂直平分线，两直线的交点即为圆心D，连接AD，CD；
（2）①根据第一问画出的图形即可得出C及D的坐标；
②在直角三角形AOD中，由OA及OD的长，利用勾股定理求出AD的长，即为圆O的半径；
③直线CE与圆O的位置关系是相切，理由为：由圆的半径得出DC的长，在直角三角形CEF中，由CF及FE的长，利用勾股定理求出CE的长，再由DE的长，利用勾股定理的逆定理得出三角形DCE为直角三角形，即EC垂直于DC，可得出直线CE为圆O的切线．

解答：解：（1）根据题意画出相应的图形，如图所示：

（2）①根据图形得：C（6，2），D（2，0）；
②在Rt△AOD中，OA=4，OD=2，
根据勾股定理得：AD=

OA2+OD2

=2

5

，
则⊙D的半径为2

5

；
③直线EC与⊙D的位置关系为相切，理由为：
在Rt△CEF中，CF=2，EF=1，
根据勾股定理得：CE=

CF2+EF2

=

5

，
在△CDE中，CD=2

5

，CE=

5

，DE=5，
∵CE²+CD²=（

5

）²+（2

5

）²=5+20=25，DE²=25，
∴CE²+CD²=DE²，
∴△CDE为直角三角形，即∠DCE=90°，
∴CE⊥DC，
则CE与圆D相切．
故答案为：（2）①（6，2）；（2，0）；②2

5

点评：此题考查了直线与圆的位置关系，涉及的知识有：坐标与图形性质，垂径定理，勾股定理及逆定理，切线的判定，利用了数形结合的思想，根据题意画出相应的图形是解本题的关键．