Question

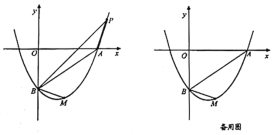
【题目】如图，抛物线与轴交于、两点（点在点的左侧），点的坐标为，与轴交于点，作直线．动点在轴上运动，过点作轴，交抛物线于点，交直线于点，设点的横坐标为．

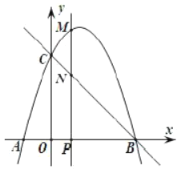
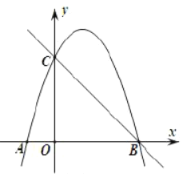
（1）直接写出抛物线的解析式__________和直线的解析式_________；

（2）当点在线段上运动时，直接写出线段长度的最大值_________；

（3）当点在线段上运动时，若是以为腰的等腰直角三角形时，求的值；

（4）当以、、、为顶点的四边形是平行四边形时，求出的值．

Answer 1

【答案】（1）y=x2+2x+3，y=x+3；（2）；（3）m=2；（4）或

【解析】

(1)由A、C两点的坐标利用待定系数法可求得抛物线解析式，则可求得B点坐标，再利用待定系数法可求得直线BC的解析式；
(2)用m可分别表示出N、M的坐标，则可表示出MN的长，再利用二次函数的最值可求得MN的最大值；
(3)由题意可得当△CMN是以MN为腰的等腰直角三角形时则有MN=MC，且MC⊥MN，则可求表示出M点坐标，代入抛物线解析式可求得m的值；
(4)由条件可得出MN=OC，结合(2)可得到关于m的方程，可求得m的值．

解：(1)∵抛物线过A、C两点，
∴代入抛物线解析式可得，解得，
∴抛物线解析式为y=x2+2x+3，
令y=0可得，x2+2x+3=0，解x1=1，x2=3，
∵B点在A点右侧，
∴B点坐标为(3,0)，
设直线BC解析式为y=kx+b，
把B、C坐标代入可得，解得，
∴直线BC解析式为y=x+3,

故答案为y=x2+2x+3，y=x+3；
(2)∵PM⊥x轴，点P的横坐标为m，
∴M(m,m2+2m+3)，N(m,m+3)，
∵P在线段OB上运动，
∴M点在N点上方，
∴MN=m2+2m+3(m+3)=m2+3m=(m )2+ ，
∴∴当m=时，MN有最大值，MN的最大值为，

故答案为；

(3)∵PM⊥x轴，
∴当△CMN是以MN为腰的等腰直角三角形时，则有CM⊥MN，
∴M点纵坐标为3，
∴m2+2m+3=3，解得m=0或m=2，
当m=0时，则M、C重合，不能构成三角形，不符合题意，舍去，
∴m=2；
(4)∵PM⊥x轴，
∴MN//OC，
当以C、O、M、N为顶点的四边形是平行四边形时，则有OC=MN，
当点P在线段OB上时，则有MN=m2+3m，
∴m2+3m=3，此方程无实数根，
当点P不在线段OB上时，则有MN=m+3(m2+2m+3)=m23m，
∴m23m=3，解得m=或m=，
综上可知当以C、O、M、N为顶点的四边形是平行四边形时，m的值为或．