题目内容
如图,⊙M与x轴相切于点C,与y轴的一个交点为A。
(1)求证:AC平分∠OAM;
(2)如果⊙M的半径等于4,∠ACO=300,求AM所在直线的解析式.

(1)求证:AC平分∠OAM;
(2)如果⊙M的半径等于4,∠ACO=300,求AM所在直线的解析式.

(1)详见解析;
(2)AM所在直线的解析式为
(2)AM所在直线的解析式为

试题分析:(1)利用切线、平行线的性质、等腰三角形的性质可证出第一问.
(2)根据勾股定理求出OA、OC长继而求出A、C点坐标,也可求出M点坐标,利用两点坐标求出直线AM的解析式.
试题解析:(1)证明:∵圆M与x轴相切于点C
连结MC,则MC⊥x轴
∴MC∥y轴
∴∠MCA=∠OAC
又∵MA= MC
∴∠MCA=∠MAC
∴∠OAC =∠MAC
即AC平分∠OAM;
(2)∵∠ACO=300,∴∠MCA= 600,
∴△MAC是等边三角形
∴AC= MC=4 ∴ 在Rt△AOC中,OA=2
即A点的坐标是(0,2)
又

∴M点的坐标是(
 ,4)
,4) 设AM所在直线的解析式为
 则
则 解得
解得 ,b="2"
,b="2" ∴AM所在直线的解析式为


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
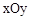 中,一次函数
中,一次函数 (a为常数)的图象与y轴相交于点A,与函数
(a为常数)的图象与y轴相交于点A,与函数 的图象相交于点B
的图象相交于点B ,
, .
.
 上一点,则点B与其对应点B′间的距离为 .
上一点,则点B与其对应点B′间的距离为 .
 的图象相交于点A(2,5)和点B,与y轴相交于点C(0,7).
的图象相交于点A(2,5)和点B,与y轴相交于点C(0,7). <
< .
.
 经过点(1,-1),求关于x的不等式2x-b≥0的解集.
经过点(1,-1),求关于x的不等式2x-b≥0的解集.


 是一次函数,则m的值是 .
是一次函数,则m的值是 .