题目内容
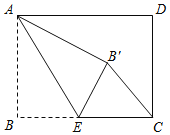
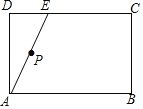
【题目】如图,矩形ABCD中,点E为矩形的边CD上的任意一点,点P为线段AE的中点,连接BP并延长与边AD交于点F,点M为边CD上的一点,且CM=DE,连接FM.
(1)依题意补全图形;
(2)求证∠DMF=∠ABF.
【答案】(1)见解析;(2)见解析.
【解析】
(1)按要求画图即可;
(2)延长BF交CD的延长线于点N,首先证明△APB和△EPN全等,得到EN=AB,再根据已知条件利用垂直平分线的性质定理证明FN=FM,可得结论.
(1)解:如图所示,

(2)证明:延长BF交CD的延长线于点N,

∵点P为线段AE中点,
∴AP=PE,
∵AB∥CD,
∴∠PEN=∠PAB,∠2=∠N,
∵在△APB和△EPN中,
∵ ,
,
∴△APB≌△EPN(AAS),
∴AB=EN
∴AB=CD=EN,
∵EN=DN+DE,CD=DM+CM,
∵DE=CM,
∴DN=DM,
∵FD⊥MN,
∴FN=FM,
∴∠N=∠1,
∴∠1=∠2,
即∠DMF=∠ABF.

练习册系列答案
相关题目