Question

【题目】综合与实践

（问题情境）

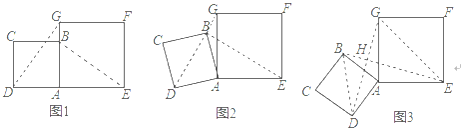
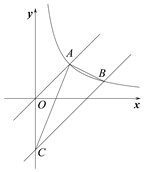
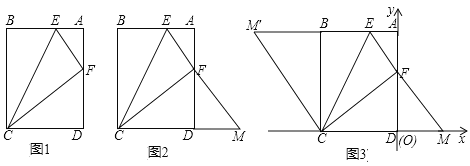
在综合与实践课上，同学们以“矩形的折叠”为主题展开数学活动，如图1，在矩形纸片ABCD中，AB=4，BC=5，点E，F分别为边AB，AD上的点，且DF=3。

（操作发现）

(1)沿CE折叠纸片，B点恰好与F点重合，求AE的长；

(2)如图2，延长EF交CD的延长线于点M，请判断△CEM的形状，并说明理由。

（深入思考）

(3)把图2置于平面直角坐标系中，如图3，使D点与原点O重合，C点在x轴的负半轴上，将△CEM沿CE翻折，使点M落在点M′处.连接CM′，求点M′的坐标.

Answer 1

【答案】(1) AE的长为；(2)ΔCEM是等腰三角形，理由见解析； (3)M′(-，5).

【解析】

（1）由矩形的性质得出∠A=90°，AD=BC=5，由折叠的性质得：FE=BE，设FE=BE=x，则AE=AB-BE=4-x，求出AF=AD-DF=5-3=2，在Rt△AEF中，由勾股定理得出方程，解方程即可；
（2）由矩形的性质得出AB∥CD，由平行线的性质得出∠BEC=∠MCE，由折叠的性质得：∠BEC=∠CEM，得出∠MCE=∠CEM，证出MC=ME即可；

（3）由平行线得出△DFM∽△AFE，得出，解得：DM=，得出ME=MC=CD+DM=，由折叠的性质得：M'E=ME=，得出AM'=M'E+AE=，即可得出答案．

(1)设AE=x.则BE=4-x

由折叠知：EF=BE=4-x

∵四边形ABCD为矩形

∴AD=BC=5

∴AF=AD-DF=5-3=2

在Rt△AEF中，由勾股定理得

AE2+AF2=EF2

即

∴

答：AE的长为；

(2)ΔCEM是等腰三角形，理由如下：

由折叠知：∠BEC=∠MEC

∵四边形ABCD为矩形

∴AB∥CD

∴∠BEC=∠MCE

∴∠MEC=∠MCE

∴ME=MC

∴ΔCEM是等腰三角形

(3)由折叠知：M′E=ME，M′C=MC

由(2)得：ME=MC

∴M′E=ME=MC=M′C

∴四边形M′CME是菱形.

由题知：E(-，5)，F(0，3)

设直线EF的解析式为y=kx+b

∴

∴

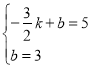
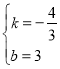
令y=0得

∴M(，0)

∴0M=

∴CM=4+=

∴M′E=MC=

∴M′A=M′E+EA=+=

∴.M′(-，5).