题目内容
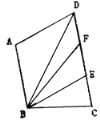
【题目】如图,AB∥CD,点E为CD上一点,连接BE,AD∥BE,连接BD,BD平分∠ABE,BF平分∠ABC交CD于点F, ∠ABC=100°，∠DBF=14°,∠ADC的度数为_______°.
【答案】72
【解析】
根据∠ABC=100°，BF平分∠ABC得到∠ABF=50°，根据∠DBF=14°得到∠ABD=36°，又BD平分∠ABE，故∠ABE=2∠ABD=72°，再根据AD∥BE，AB∥CD即可求解∠ADC.
∵∠ABC=100°，BF平分∠ABC
∴∠ABF=
∠ABC=50°，
∵∠DBF=14°
∴∠ABD=∠ABF -∠DBF =36°，
又BD平分∠ABE，
∴∠ABE=2∠ABD=72°，
∵AD∥BE，∴∠BAD=180°-∠ABE=108°，
∵AB∥CD
∴∠ADC=180°-∠BAD =72°
故填：72.
练习册系列答案
名题金卷系列答案
优加精卷系列答案
相关题目
