题目内容
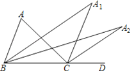
【题目】如图,在△ABC中,∠A=48°,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;……;∠An-1BC与∠An-1CD的平分线交于点An,要使∠An的度数为整数,则n的最大值为( )
A.2B.3C.4D.5
【答案】C
【解析】
由三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠ABC+∠A,∠A1CD=∠A1BC+∠A1,根据角平分线的定义可得∠A1BC=![]() ∠ABC,∠A1CD=
∠ABC,∠A1CD=![]() ∠ACD,然后整理得到∠A1=
∠ACD,然后整理得到∠A1=![]() ∠A,根据A1B、A1C分别平分∠ABC、∠ACD可得:∠ABC=2∠A1BC,∠ACD=2∠A1CD,而∠ACD=∠A+∠ABC ,∠A1CD=∠A1+∠A1BC,于是有∠A=2∠A1,同理可得∠A1=2∠A2,继而∠A2=
∠A,根据A1B、A1C分别平分∠ABC、∠ACD可得:∠ABC=2∠A1BC,∠ACD=2∠A1CD,而∠ACD=∠A+∠ABC ,∠A1CD=∠A1+∠A1BC,于是有∠A=2∠A1,同理可得∠A1=2∠A2,继而∠A2=![]() ∠A,因此发现规律,将∠A代入即可求出使∠An的度数为整数,则n的最大值.
∠A,因此发现规律,将∠A代入即可求出使∠An的度数为整数,则n的最大值.
由三角形的外角性质可得:∠ACD=∠ABC+∠A,∠A1CD=∠A1BC+∠A1,
∵∠ABC与∠ACD的平分线交于点A1,
∴∠A1BC=![]() ∠ABC,∠A1CD=
∠ABC,∠A1CD=![]() ∠ACD,
∠ACD,
∴∠A1+∠A1BC=∠A1CD =![]() (∠ABC+∠A)=
(∠ABC+∠A)=![]() ∠A+∠A1BC,
∠A+∠A1BC,
∴∠A1=![]() ∠A=
∠A=![]() ×48°=24°,
×48°=24°,
∵A1B、A1C分别平分∠ABC、∠ACD,
∴∠ABC=2∠A1BC,∠ACD=2∠A1CD,
而∠ACD=∠A+∠ABC ,∠A1CD=∠A1+∠A1BC,
∴∠A=2∠A1,
∴∠A1=![]() ∠A,
∠A,
同理可得:∠A1=2∠A2,
∴∠A2=![]() ∠A,
∠A,
∴∠A=2n∠An,
∴∠An=![]() ∠A
∠A
∵∠A=48°
∴当n=4时,∠A4=![]() ×48°=3°,此时n的值最大,
×48°=3°,此时n的值最大,
故选:C

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目