题目内容
如图,在矩形ABCD中,对角线AC、BD交于点O,∠AOD=120°,AB=1,则AC=______;AD=______.
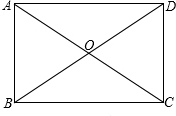

∵ABCD是矩形,
∴OA=OB.
∵∠AOD=120°,
∴∠AOB=60°.
∴△AOB为等边三角形.
∵AC=BD,
∴AO=BO=AB=1.
∴AC=2AO=2.
∵AC=2,DC=AB=1,
∴AD2=AC2-DC2=4-1=3.
∴AD=
故答案为2,
.
∴OA=OB.
∵∠AOD=120°,
∴∠AOB=60°.
∴△AOB为等边三角形.
∵AC=BD,
∴AO=BO=AB=1.
∴AC=2AO=2.
∵AC=2,DC=AB=1,
∴AD2=AC2-DC2=4-1=3.
∴AD=
| 3 |
故答案为2,
| 3 |

练习册系列答案
相关题目



 .
.