题目内容
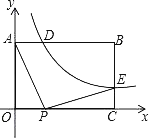
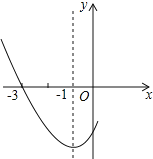
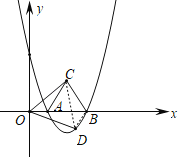
【题目】如图,抛物线y=![]() 与x轴交于A、B两点,△ABC为等边三角形,∠COD=60°,且OD=OC.
与x轴交于A、B两点,△ABC为等边三角形,∠COD=60°,且OD=OC.
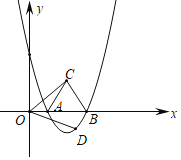
(1)A点坐标为 ,B点坐标为 ;
(2)求证:点D在抛物线上;
(3)点M在抛物线的对称轴上,点N在抛物线上,若以M、N、O、D为顶点的四边形为平行四边形,请直接写出点M的坐标.
【答案】(1)(2,0),(5,0);(2)见解析;(3)点M的坐标为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)y=![]() ,令y=0,解得:x=2或5,即可求解;
,令y=0,解得:x=2或5,即可求解;
(2)证明△OAC≌△DBC(SAS),则BD=OA=2,∠OBD=60°,即可求解;
(3)分OD是平行四边形的边、OD是平行四边形的对角线两种情况,分别求解.
解:(1)y=![]() ,令y=0,解得:x=2或5,
,令y=0,解得:x=2或5,
故A点坐标为:(2,0)、B点坐标为(5,0);
(2)连接CD、BD,
由(1)知:OA=2,AB=3,等边三角形ABC的边长为3,
∵△ABC为等边三角形,
∴AC=BC,∠ACB=60°=∠CAB,∴∠CAO=120°,
∵∠COD=60°,且OD=OC,则△OCD为等边三角形,
∴OD=CD=CO,则∠OCD=60°=∠OCA+∠ACD,
而∠ACB=60°=∠ACD+∠DCB,
∴∠OCA=∠DCB,
而CO=CD,CA=CB,
∴△OAC≌△DBC(SAS),
∴BD=OA=2,∠CBD=∠CAO=120°,而∠CBO=60°,
∴∠OBD=60°,则yD=﹣BDsin∠OBD=﹣2×![]() =﹣
=﹣![]() ,
,
故点D的坐标为(4,﹣![]() ),
),
当x=4时,y=![]() =﹣
=﹣![]() ,
,
故点D在抛物线上;
(3)抛物线的对称轴为:x=![]() ,
,
设点M(![]() ,s),点N(m,n),
,s),点N(m,n),
n=![]() m2﹣
m2﹣![]() m+5
m+5![]() ,
,
①当OD是平行四边形的边时,
当点N在对称轴右侧时,
点O向右平移4个单位,向下平移![]() 个单位得到D,
个单位得到D,
同样点M向右平移4个单位,向下平移![]() 个单位得到N,
个单位得到N,
即:![]() +4=m,s﹣
+4=m,s﹣![]() =n,而n=
=n,而n=![]() m2﹣
m2﹣![]() m+5
m+5![]() ,
,
解得:s=![]()
则点M(![]() ,
,![]() );
);
当点N在对称轴左侧时,
同理可得:点M(![]() ,
,![]() );
);
②当OD是平行四边形的对角线时,
则4=![]() +m,﹣
+m,﹣![]() =n+s,而n=
=n+s,而n=![]() m2﹣
m2﹣![]() m+5
m+5![]() ,
,
解得:s=![]() ,
,
则点M(![]() ,
,![]() ),
),
故点M的坐标为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

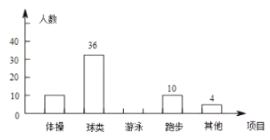
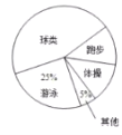
【题目】某校为选拔一名选手参加“美丽邵阳,我为家乡做代言”主题演讲比赛,经研究,按图所示的项目和权数对选拔赛参赛选手进行考评(因排版原因统计图不完整).下表是李明、张华在选拔赛中的得分情况:
项目 选手 | 服装 | 普通话 | 主题 | 演讲技巧 |
李明 | 85 | 70 | 80 | 85 |
张华 | 90 | 75 | 75 | 80 |
结合以上信息,回答下列问题:
(1)求服装项目的权数及普通话项目对应扇形的圆心角大小;
(2)求李明在选拔赛中四个项目所得分数的众数和中位数;
(3)根据你所学的知识,帮助学校在李明、张华两人中选择一人参加“美丽邵阳,我为家乡做代言”主题演讲比赛,并说明理由.