题目内容
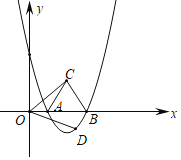
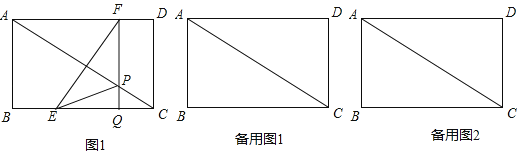
【题目】如图1，在矩形ABCD中，AB＝6cm，BC＝8cm，如果点E由点B出发沿BC方向向点C匀速运动，同时点F由点D出发沿DA方向向点A匀速运动，它们的速度分别为每秒2cm和1cm，FQ⊥BC，分别交AC、BC于点P和Q，设运动时间为t秒（0＜t＜4）．
（1）连接EF，若运动时间t＝
秒时，求证：△EQF是等腰直角三角形；
（2）连接EP，当△EPC的面积为3cm2时，求t的值；
（3）在运动过程中，当t取何值时，△EPQ与△ADC相似．
【答案】（1）详见解析；（2）2秒；（3）2秒或
秒或
秒．
【解析】
（1）由题意通过计算发现EQ＝FQ＝6，由此即可证明；
（2）根据题意利用三角形的面积建立方程即可得出结论；
（3）由题意分点E在Q的左侧以及点E在Q的右侧这两种情况，分别进行分析即可得出结论．
解：（1）证明：若运动时间t＝
秒，则
BE＝2×＝
（cm），DF＝（cm），
∵四边形ABCD是矩形
∴AD＝BC＝8（cm），AB＝DC＝6（cm），∠D＝∠BCD＝90°
∵∠D＝∠FQC＝∠QCD＝90°，
∴四边形CDFQ也是矩形，
∴CQ＝DF，CD＝QF＝6（cm），
∴EQ＝BC﹣BE﹣CQ＝8﹣﹣＝6（cm），
∴EQ＝QF＝6（cm），
又∵FQ⊥BC，
∴△EQF是等腰直角三角形；
（2）由（1）知，CE＝8﹣2t，CQ＝t，
在Rt△ABC中，tan∠ACB＝
＝
，
在Rt△CPQ中，tan∠ACB＝
＝
＝，
∴PQ＝t，
∵△EPC的面积为3cm2，
∴S△EPC＝
CE×PQ＝×（8﹣2t）×t＝3，
∴t＝2秒，
即t的值为2秒；
（3）解：分两种情况：
Ⅰ．如图1中，点E在Q的左侧．
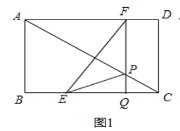
①∠PEQ=∠CAD时，△EQP∽△ADC，
∵四边形ABCD是矩形，
∴AD∥BC，
∴∠CAD=∠ACB，
∵△EQP∽△ADC，
∴∠CAD=∠QEP，
∴∠ACB=∠QEP，
∴EQ=CQ，
∴CE=2CQ，
由（1）知，CQ=t，CE=8-2t，
∴8-2t=2t，
∴t=2秒；
②∠PEQ=∠ACD时，△EPQ∽△CAD，
∴
，
∵FQ⊥BC，
∴FQ∥AB，
∴△CPQ∽△CAB，
∴
，即
，
解得：
，
∴
，
解得：
；
Ⅱ．如图2中，点E在Q的右侧．
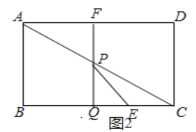
∵0＜t＜4，
∴点E不能与点C重合，
∴只存在△EPQ∽△CAD，
可得，即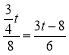
，
解得：
；
综上所述，t的值为2秒或秒或秒时，△EPQ与△ADC相似．
