题目内容
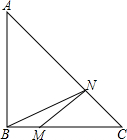 已知:如图Rt△ABC中,∠B=90°,AB=BC=8,M在BC上,且BM=2,N是AC上一动点,则BN+MN的最小值为
已知:如图Rt△ABC中,∠B=90°,AB=BC=8,M在BC上,且BM=2,N是AC上一动点,则BN+MN的最小值为分析:根据平面内线段最短,构建直角三角形,解直角三角形即可.
解答: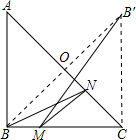 解:过点B作BO⊥AC于O,延长BO到B',使OB'=OB,连接MB',交AC于N,
解:过点B作BO⊥AC于O,延长BO到B',使OB'=OB,连接MB',交AC于N,
此时MB'=MN+NB'=MN+BN的值最小,
连接CB',
∵BO⊥AC,AB=BC,∠ABC=90°,
∴∠CBO=
×90°=45°,
∵BO=OB',BO⊥AC,
∴CB'=CB,
∴∠CB'B=∠OBC=45°,
∴∠B'CB=90°,
∴CB'⊥BC,
根据勾股定理可得MB′=1O,MB'的长度就是BN+MN的最小值.
 解:过点B作BO⊥AC于O,延长BO到B',使OB'=OB,连接MB',交AC于N,
解:过点B作BO⊥AC于O,延长BO到B',使OB'=OB,连接MB',交AC于N,此时MB'=MN+NB'=MN+BN的值最小,
连接CB',
∵BO⊥AC,AB=BC,∠ABC=90°,
∴∠CBO=
| 1 |
| 2 |
∵BO=OB',BO⊥AC,
∴CB'=CB,
∴∠CB'B=∠OBC=45°,
∴∠B'CB=90°,
∴CB'⊥BC,
根据勾股定理可得MB′=1O,MB'的长度就是BN+MN的最小值.
点评:此题考查了线路最短的问题,确定动点E何位置时,使BN+MN的值最小是关键.

练习册系列答案
相关题目


 已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4.
已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4. 已知:如图Rt△ABC中,∠C=Rt∠,AB=5,BC=4.
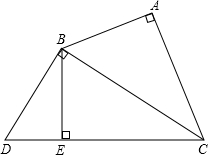
已知:如图Rt△ABC中,∠C=Rt∠,AB=5,BC=4. 已知:如图Rt△ABD和Rt△BCD如图放置,∠BAD=∠BCD=90°,连接AC,若AC平分∠DAB,则线段AB、AD、AC有怎样的数量关系?写出你的猜想,并证明.
已知:如图Rt△ABD和Rt△BCD如图放置,∠BAD=∠BCD=90°,连接AC,若AC平分∠DAB,则线段AB、AD、AC有怎样的数量关系?写出你的猜想,并证明.