题目内容
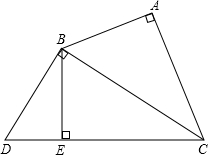 已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4.
已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4.(1)求BD、CD的长;
(2)过B作BE⊥DC于E,求BE的长.
分析:(1)由勾股定理可得BC的长,根据相似三角形的对应边成比例可求出BD、CD的长;
(2)根据△BCD面积的不同表示方法,即可求出BE的长.
(2)根据△BCD面积的不同表示方法,即可求出BE的长.
解答:解:(1)Rt△ABC中,根据勾股定理得:
BC=
=5,
∵Rt△ABC∽Rt△BDC,
∴
=
=
,
=
=
,
∴BD=
,CD=
;
(2)在Rt△BDC中,
S△BDC=
BE•CD=
BD•BC,
∴BE=
=
=3.
BC=
| AB2+AC2 |
∵Rt△ABC∽Rt△BDC,
∴
| AB |
| BD |
| BC |
| DC |
| AC |
| BC |
| 3 |
| BD |
| 5 |
| DC |
| 4 |
| 5 |
∴BD=
| 15 |
| 4 |
| 25 |
| 4 |
(2)在Rt△BDC中,
S△BDC=
| 1 |
| 2 |
| 1 |
| 2 |
∴BE=
| BD•BC |
| CD |
| ||
|
点评:本题主要考查的是直角三角形的性质及直角三角形面积的不同表示方法.

练习册系列答案
相关题目


 已知:如图Rt△ABC中,∠C=Rt∠,AB=5,BC=4.
已知:如图Rt△ABC中,∠C=Rt∠,AB=5,BC=4.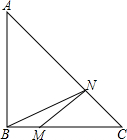 已知:如图Rt△ABC中,∠B=90°,AB=BC=8,M在BC上,且BM=2,N是AC上一动点,则BN+MN的最小值为
已知:如图Rt△ABC中,∠B=90°,AB=BC=8,M在BC上,且BM=2,N是AC上一动点,则BN+MN的最小值为 已知:如图Rt△ABD和Rt△BCD如图放置,∠BAD=∠BCD=90°,连接AC,若AC平分∠DAB,则线段AB、AD、AC有怎样的数量关系?写出你的猜想,并证明.
已知:如图Rt△ABD和Rt△BCD如图放置,∠BAD=∠BCD=90°,连接AC,若AC平分∠DAB,则线段AB、AD、AC有怎样的数量关系?写出你的猜想,并证明.