题目内容
 已知:如图Rt△ABC中,∠C=Rt∠,AB=5,BC=4.
已知:如图Rt△ABC中,∠C=Rt∠,AB=5,BC=4.(1)求AC的长度.
(2)有一动点P从点C开始沿C→B→A方向以1cm∕s的速度运动,到达点A后停止运动,设运动时间为t秒.求:
①当t为几秒时,AP平分∠CAB.
②当t为几秒时,△ACP是等腰三角形(直接写出答案).
分析:(1)直接运用勾股定理就可以求出AC的值;
(2)①如图1,当AP平分∠CAB时,作PE⊥AB于E,由勾股定理就可以求出t的值;
②分3种情况如图2,当AC=PC时,可以求出t=4,如图3,当AP=CP时,作PE⊥AC,于点E,由等腰三角形的性质就可以得出E是AC的中点,进而得出P是AB 的中点,就可以求出t=6.5,如图4,当AC=AP时,就可以求出t=6.
(2)①如图1,当AP平分∠CAB时,作PE⊥AB于E,由勾股定理就可以求出t的值;
②分3种情况如图2,当AC=PC时,可以求出t=4,如图3,当AP=CP时,作PE⊥AC,于点E,由等腰三角形的性质就可以得出E是AC的中点,进而得出P是AB 的中点,就可以求出t=6.5,如图4,当AC=AP时,就可以求出t=6.
解答:解:(1)在Rt△ABC中,由勾股定理,得
AC=
=
=3.
答:AC=3;
(2)①作PE⊥AB于E,
∴∠AEP=∠BEP=90°
∵PC⊥AC,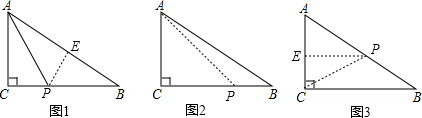
∴∠C=90°,PC=PE.
∴∠C=∠AEP.
∵AP平分∠CAB,
∴∠PAC=∠PAE.
在△ACP和△AEP中,
,
∴△ACP≌△AEP(AAS),
∴AC=AE=3,
∴BE=2.
∵PC=t秒,
∴PE=t秒,PB=(4-t)秒.
在Rt△PEB中,由勾股定理,得
t2+22=(4-t)2,
解得:t=1.5秒.
②如图2,当AC=PC时,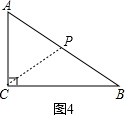
∴PC=t=4秒;
如图3,当AP=CP时,作PE⊥AC于E,
∴∠AEP=90°,AE=CE.
∵∠ACB=90°,
∴∠AEP=∠ACB,
∴EP∥AB,
∴AP=BP,
∴BP=2.5,
∴t=4+2.5=6.5秒;
如图4,当AP=AC时,
∴AP=3,
∴PB=2,
∴t=4+2=6秒.
∴当t=4秒,6秒或6.5秒时△ACP为等腰三角形.
AC=
| AB2-BC2 |
| 52-4 2 |
答:AC=3;
(2)①作PE⊥AB于E,
∴∠AEP=∠BEP=90°
∵PC⊥AC,

∴∠C=90°,PC=PE.
∴∠C=∠AEP.
∵AP平分∠CAB,
∴∠PAC=∠PAE.
在△ACP和△AEP中,
|
∴△ACP≌△AEP(AAS),
∴AC=AE=3,
∴BE=2.
∵PC=t秒,
∴PE=t秒,PB=(4-t)秒.
在Rt△PEB中,由勾股定理,得
t2+22=(4-t)2,
解得:t=1.5秒.
②如图2,当AC=PC时,

∴PC=t=4秒;
如图3,当AP=CP时,作PE⊥AC于E,
∴∠AEP=90°,AE=CE.
∵∠ACB=90°,
∴∠AEP=∠ACB,
∴EP∥AB,
∴AP=BP,
∴BP=2.5,
∴t=4+2.5=6.5秒;
如图4,当AP=AC时,
∴AP=3,
∴PB=2,
∴t=4+2=6秒.
∴当t=4秒,6秒或6.5秒时△ACP为等腰三角形.
点评:本题考查了勾股定理的运用,角平分线的性质的运用,全等三角形的判定及性质的运用,等腰三角形的性质的运用,解答时运用勾股定理求值是关键.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目


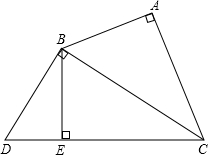 已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4.
已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4.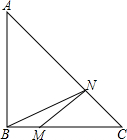 已知:如图Rt△ABC中,∠B=90°,AB=BC=8,M在BC上,且BM=2,N是AC上一动点,则BN+MN的最小值为
已知:如图Rt△ABC中,∠B=90°,AB=BC=8,M在BC上,且BM=2,N是AC上一动点,则BN+MN的最小值为 已知:如图Rt△ABD和Rt△BCD如图放置,∠BAD=∠BCD=90°,连接AC,若AC平分∠DAB,则线段AB、AD、AC有怎样的数量关系?写出你的猜想,并证明.
已知:如图Rt△ABD和Rt△BCD如图放置,∠BAD=∠BCD=90°,连接AC,若AC平分∠DAB,则线段AB、AD、AC有怎样的数量关系?写出你的猜想,并证明.