题目内容
在矩形ABCD中，AB=4，BC=10，点M在BC上．
（1）若BM=3时，求点D到直线AM的距离；
（2）若AM⊥DM，求BM的长．
（1）若BM=3时，求点D到直线AM的距离；
（2）若AM⊥DM，求BM的长．
（1）如图（2），
过点D作DH⊥AM垂足为H，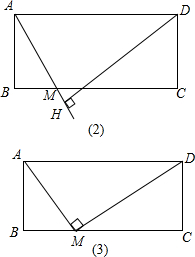
∵AB=4，BM=3
∴AM=5．
∴sin∠DAM=sin∠AMB=
=
，
∴DH=
×10=8，
（2）如图（3）
∵AM⊥DM，
∴∠AMB+∠DMC=90°，
∵∠AMB+∠BAM=90°
∴∠BAM=∠DMC
∴△ABM∽△MCD，
∴
=
=
∴BM2-10BM+16=0，解得，BM=2或BM=8．
过点D作DH⊥AM垂足为H，
∵AB=4，BM=3
∴AM=5．
∴sin∠DAM=sin∠AMB=
| 4 |
| 5 |
| DH |
| 10 |
∴DH=
| 4 |
| 5 |
（2）如图（3）
∵AM⊥DM，
∴∠AMB+∠DMC=90°，
∵∠AMB+∠BAM=90°
∴∠BAM=∠DMC
∴△ABM∽△MCD，
∴
| BM |
| DC |
| AB |
| MC |
| BM |
| 4 |
| 4 |
| 10-BM |
∴BM2-10BM+16=0，解得，BM=2或BM=8．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南师范大学出版社系列答案
补充习题江苏系列答案
相关题目
