题目内容
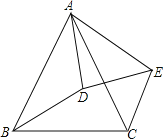
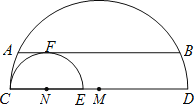
【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°.以AB长为一边作△ABD,且AD=BD,∠ADB=90°,取AB中点E,连DE、CE、CD.则∠EDC= °.

【答案】75
【解析】
试题分析:根据在直角三角形中,斜边上的中线等于斜边的一半得到EC=EA=EB=![]() AB,根据三角形的外角的性质求出∠CEB=60°,根据直角三角形的性质得到ED=EC,根据三角形内角和定理计算即可.
AB,根据三角形的外角的性质求出∠CEB=60°,根据直角三角形的性质得到ED=EC,根据三角形内角和定理计算即可.
解:∵∠ACB=90°,点E是AB中点,
∴EC=EA=EB=![]() AB,
AB,
∴∠ECA=∠CAB=30°,
∴∠CEB=60°,
∵AD=BD,点E是AB中点,
∴DE⊥AB,即∠AED=90°,
∴∠DEC=180°﹣90°﹣60°=30°,
∵∠ADB=90°,点E是AB中点,
∴DE=![]() AB,
AB,
∴ED=EC,
∴∠EDC=75°,
故答案为:75.

练习册系列答案
相关题目