题目内容
【题目】已知⊙O的直径AB=4,点C在⊙O上,连接AC,沿AC折叠劣弧![]() ,记折叠后的劣弧为
,记折叠后的劣弧为![]() .
.
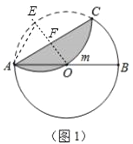
(1)如图1,当![]() 经过圆心O时,求
经过圆心O时,求![]() 的长.
的长.
(2)如图2,当![]() 与AB相切于A时.
与AB相切于A时.
①画出![]() 所在的圆的圆心P.
所在的圆的圆心P.
②求出阴影部分弓形![]() 的面积.
的面积.


【答案】(1)![]() ;(2)π﹣2.
;(2)π﹣2.
【解析】
(1)只要证明△EA O是等边三角形即可解决问题;
(2)①过A点作AP⊥AB,再截取AP=2,则P点为所求,如图2;
②只要证明四边形AOCP是正方形即可解决问题.
(1)作半径OE⊥AC于F,连接AE,如图1,
∵沿AC折叠劣弧![]() ,记折叠后的劣弧为
,记折叠后的劣弧为![]() ,
,
∴OF=![]() OE=OF,
OE=OF,
∵OE⊥AC,
∴AE=AO,
∵OA=OE,
∴AE=AO=OE,
∴△AOE是等边三角形,
∴∠AEO=60°,
∴![]() 的长=
的长=![]() ;
;
(2)①过A点作AP⊥AB,再截取AP=2,则P点为所求,如图2;
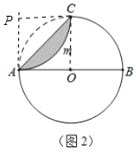
②连结PC、OC,
∵AP=OA=OC=PC=2,
∴四边形PAOC为菱形,
而∠PAO=90°,
∴四边形PAOC为正方形,
∴S阴=![]() ×2×2=π﹣2.
×2×2=π﹣2.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目