题目内容
【题目】在等边△ABC中,E为BC边上一点,G为BC延长线上一点,过点E作∠AEM=60°,交∠ACG的平分线于点M.

(1)如图1,当点E在BC边的中点位置时,求证:AE=EM;
(2)如图2,当点E在BC边的任意位置时,(1)中的结论是否成立?请说明理由.
【答案】(1)见解析;(2)(1)中的结论成立,理由见解析.
【解析】
(1)取AB的中点N,连接EN,可证明△ANE≌△ECM,可证得AE=EM;
(2)在AB上取点H,使BH=BE,根据等边三角形的证明△AHE≌△ECM即可求解.
(1)证明:取AB的中点N,连接EN,
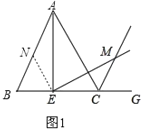
∵△ABC为等边三角形,E,N为中点,
∴AE⊥BC,且AE平分∠BAC,
∴AN=NE=EC,∠NAE=∠NEA=30°,∴∠ANE=120°,
∵∠AEM=60°,∴∠MEC=30°,∴∠NAE=∠CEM,
∵CM平分∠ACG,∴∠ACM=60°,∴∠ECM=∠ANE=120°,
在△ANE和△ECM中,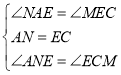 ,∴△ANE≌△ECM(ASA),
,∴△ANE≌△ECM(ASA),
∴AE=EM;
(2)在AB上取点H,使BH=BE,
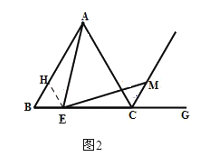
∵△ABC是等边三角形,∴AB=BC,∠B=60°.
∵BH=BE,∴AH=CE.
∴△BHE是等边三角形,∴∠BHE=60°.∴∠AHE=120°.
∵∠ECM=120°.∴∠AHE=∠ECM.
∵∠AEM+∠MEC=∠ABC+∠EAH,∴∠EAH=∠MEC
在△AHE和△ECM中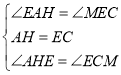 ,∴△AHE≌△ECM(ASA).
,∴△AHE≌△ECM(ASA).
∴AE=EM.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目






