题目内容
 如图,已知O为原点,点A的坐标为(4,3),⊙A的半径为2,过A作直线L平行于x轴,点P在直线L上运动.
如图,已知O为原点,点A的坐标为(4,3),⊙A的半径为2,过A作直线L平行于x轴,点P在直线L上运动.(1)当点P在⊙A上时,请直接写出它的坐标;
(2)设点P的横坐标为6
| 2 |
分析:(1)由题意知,点P的纵坐标与点B的纵坐标相同,即为3;当点P在BA之间时,它的横坐标为4-2=2;当点在BA的延长线上时,它的横坐标为4+2=6.
(2)连接OP,过点A作AC⊥OP,垂足为C.则有△APC∽△OPB,求得AC的值,与圆A的半径比较,即可得到OP与圆A的位置关系.
(2)连接OP,过点A作AC⊥OP,垂足为C.则有△APC∽△OPB,求得AC的值,与圆A的半径比较,即可得到OP与圆A的位置关系.
解答: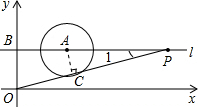 解:(1)点P的坐标是(2,3)或(6,3).
解:(1)点P的坐标是(2,3)或(6,3).
(2)连接OP,过点A作AC⊥OP,垂足为C.
那么AP=PB-AB=6
-4,OB=3,
OP=
=9.
∵∠ACP=∠OBP=90°,∠1=∠1,
∴△APC∽△OPB.
∴
=
.
∴
=
.
∴AC=2
-
≈1.5<2.
∴直线OP与⊙A相交.
 解:(1)点P的坐标是(2,3)或(6,3).
解:(1)点P的坐标是(2,3)或(6,3).(2)连接OP,过点A作AC⊥OP,垂足为C.
那么AP=PB-AB=6
| 2 |
OP=
(6
|
∵∠ACP=∠OBP=90°,∠1=∠1,
∴△APC∽△OPB.
∴
| AC |
| OB |
| AP |
| OP |
∴
| AC |
| 3 |
6
| ||
| 9 |
∴AC=2
| 2 |
| 4 |
| 3 |
∴直线OP与⊙A相交.
点评:此题主要考查了直线和圆位置关系应用的典型题目,解题的关键是作出圆心到直线的距离,利用勾股定理和相似三角形的性质求得此值,再进行判断,难度中等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
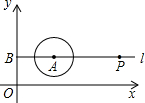 点B,点P在直线l上运动.
点B,点P在直线l上运动.
 点P在直线l上运动.
点P在直线l上运动.