题目内容
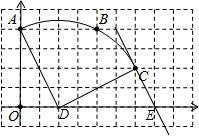
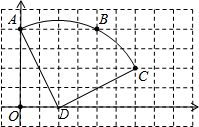
如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
(1)请完成如下操作:①以点O为原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,标出该圆弧所在圆的圆心D,并连接AD、CD.
(2)请在(1)的基础上,完成下列填空:
①写出点的坐标:C______;D(______);
②⊙D的半径=______(结果保留根号);
③若扇形ADC是一个圆锥的侧面展开图,则该圆锥的底面的面积为______;(结果保留π)
④若E(7,0),试判断直线EC与⊙D的位置关系,并说明你的理由.
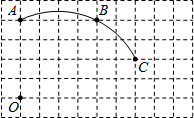
(1)请完成如下操作:①以点O为原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,标出该圆弧所在圆的圆心D,并连接AD、CD.
(2)请在(1)的基础上,完成下列填空:
①写出点的坐标:C______;D(______);
②⊙D的半径=______(结果保留根号);
③若扇形ADC是一个圆锥的侧面展开图,则该圆锥的底面的面积为______;(结果保留π)
④若E(7,0),试判断直线EC与⊙D的位置关系,并说明你的理由.

(1)C(6,2);D(2,0);(各得1分)
(2)⊙D的半径=
=
=2
;( 1分)
(3)AC=
=2
,CD=2
,
AD2+CD2=AC2,∴∠ADC=90°.
扇形ADC的弧长=
=
π,
圆锥的底面的半径=
,
圆锥的底面的面积为π(
)2=
;(1分)
(4)直线EC与⊙D相切.(1分)
证明:∵CD2+CE2=DE2=25,(2分)
∴∠DCE=90°.(1分)
∴直线EC与⊙D相切(1分).
(2)⊙D的半径=
| OA2+OD2 |
| 16+4 |
| 5 |
(3)AC=
| 22+62 |
| 10 |
| 5 |
AD2+CD2=AC2,∴∠ADC=90°.
扇形ADC的弧长=
90•π•2
| ||
| 180 |
| 5 |
圆锥的底面的半径=
| ||
| 2 |
圆锥的底面的面积为π(
| ||
| 2 |
| 5π |
| 4 |

(4)直线EC与⊙D相切.(1分)
证明:∵CD2+CE2=DE2=25,(2分)
∴∠DCE=90°.(1分)
∴直线EC与⊙D相切(1分).


练习册系列答案
相关题目

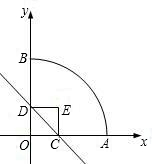 标系.如图所示、正方形两个顶点C、D分别在x轴、y轴正半轴上移动、设OC=x,OA=3,则:
标系.如图所示、正方形两个顶点C、D分别在x轴、y轴正半轴上移动、设OC=x,OA=3,则: