题目内容
正方形OCED与扇形OAB有公共顶点O,分别以OA、OB所在直线为x轴,y轴建立平面直角坐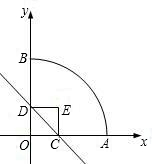 标系.如图所示、正方形两个顶点C、D分别在x轴、y轴正半轴上移动、设OC=x,OA=3,则:
标系.如图所示、正方形两个顶点C、D分别在x轴、y轴正半轴上移动、设OC=x,OA=3,则:
(1)当x=1时,正方形与扇形不重合的面积是______;
(2)当x=______时,直线CD与扇形OAB相切,此时切点坐标是______;
(3)当正方形有顶点恰好落在AB上时,求正方形与扇形不重合的面积.
 标系.如图所示、正方形两个顶点C、D分别在x轴、y轴正半轴上移动、设OC=x,OA=3,则:
标系.如图所示、正方形两个顶点C、D分别在x轴、y轴正半轴上移动、设OC=x,OA=3,则:(1)当x=1时,正方形与扇形不重合的面积是______;
(2)当x=______时,直线CD与扇形OAB相切,此时切点坐标是______;
(3)当正方形有顶点恰好落在AB上时,求正方形与扇形不重合的面积.
(1)当x=1时,正方形与扇形不重合的面积是:
-1;
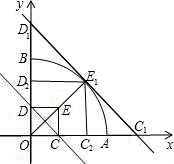 (2)如图,当直线CD与扇形OAB相切时,设切线为C1D1,切点为E1,
(2)如图,当直线CD与扇形OAB相切时,设切线为C1D1,切点为E1,
根据切线的性质得,OE1=OA=3,OE1⊥C1D1,
又∵C1D1∥CD,∴∠E1C10=∠DCO=45°,
∴OC2,=C2E1=OE1•sin45°=
,
即切点E1坐标为(
,
);
(3)①如图,当正方形有顶点恰好落在AB上时,正方形对角线OE1=OA=3,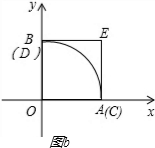
不重合部分面积为:
-
×3×3=
-
.
②如图b,当点C,D分别与A,B重合时,OC=OA=3,
∴不重合部分面积为:S正方形OCED-S扇形AOB=9-
π.
| 9π |
| 4 |
 (2)如图,当直线CD与扇形OAB相切时,设切线为C1D1,切点为E1,
(2)如图,当直线CD与扇形OAB相切时,设切线为C1D1,切点为E1,根据切线的性质得,OE1=OA=3,OE1⊥C1D1,
又∵C1D1∥CD,∴∠E1C10=∠DCO=45°,
∴OC2,=C2E1=OE1•sin45°=
3
| ||
| 2 |
即切点E1坐标为(
3
| ||
| 2 |
3
| ||
| 2 |
(3)①如图,当正方形有顶点恰好落在AB上时,正方形对角线OE1=OA=3,

不重合部分面积为:
| 9π |
| 4 |
| 1 |
| 2 |
| 9π |
| 4 |
| 9 |
| 2 |
②如图b,当点C,D分别与A,B重合时,OC=OA=3,
∴不重合部分面积为:S正方形OCED-S扇形AOB=9-
| 9 |
| 4 |

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目