题目内容
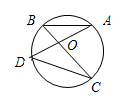
如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC,垂足为E。
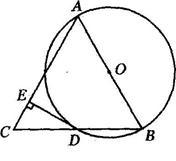
(1)求证:DE为⊙O的切线;
(2)若⊙O的半径为5,∠BAC=60°,求DE的长.

(1)求证:DE为⊙O的切线;
(2)若⊙O的半径为5,∠BAC=60°,求DE的长.
(1)见解析(2) 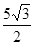
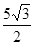
(1)证明:如图D2-2,连结OD.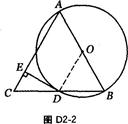
∵OA=OB,CD=BD,∴OD∥AC.
∴∠0DE=∠CED.
又∵DE⊥AC,∴∠CED=90°.∴∠ODE=90°,即OD⊥DE.
∴DE是⊙O的切线.
(2)解:∵OD∥AC,∠BAC=60°,∴∠BOD=∠BAC=60°,
∠C=∠0DB.
又∵OB=OD,∴△BOD是等边三角形.
∴∠C=∠ODB=60°,CD=BD=5.
∵DE⊥AC,∴DE=CD·sin∠C =5×sin60°=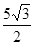 .
.
(1)连接OD,根据OA=OB,CD=BD,得出OD∥AC,∠0DE=∠CED,再根据DE⊥AC,即可证出OD⊥DE,从而得出答案;
(2)结合(1)中的结论,可以证明△BOD是等边三角形,即可求得CD和BD的长,再根据锐角三角函数即可计算DE的长.

∵OA=OB,CD=BD,∴OD∥AC.
∴∠0DE=∠CED.
又∵DE⊥AC,∴∠CED=90°.∴∠ODE=90°,即OD⊥DE.
∴DE是⊙O的切线.
(2)解:∵OD∥AC,∠BAC=60°,∴∠BOD=∠BAC=60°,
∠C=∠0DB.
又∵OB=OD,∴△BOD是等边三角形.
∴∠C=∠ODB=60°,CD=BD=5.
∵DE⊥AC,∴DE=CD·sin∠C =5×sin60°=
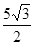 .
. (1)连接OD,根据OA=OB,CD=BD,得出OD∥AC,∠0DE=∠CED,再根据DE⊥AC,即可证出OD⊥DE,从而得出答案;
(2)结合(1)中的结论,可以证明△BOD是等边三角形,即可求得CD和BD的长,再根据锐角三角函数即可计算DE的长.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
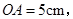 弦
弦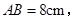 点
点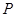 为弦
为弦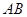 上一动点,则点
上一动点,则点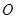 的最短距离是 cm.
的最短距离是 cm. 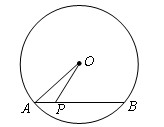
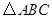 的外接圆,
的外接圆,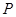 是⊙O上一点,则
是⊙O上一点,则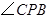 等于( )
等于( )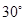
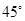
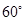
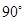

 和⊙
和⊙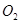 的半径分别为10
的半径分别为10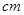 和4
和4