题目内容
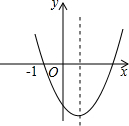
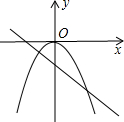
己知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
(1)a-b+c>0
(2)方程ax2+bx+c=0两根之和大于零
(3)y随x的增大而增大
(4)一次函数y=x+bc的图象一定不过第四象限.其中正确的个数是( )

(1)a-b+c>0
(2)方程ax2+bx+c=0两根之和大于零
(3)y随x的增大而增大
(4)一次函数y=x+bc的图象一定不过第四象限.其中正确的个数是( )
| A.1个 | B.2个 | C.3个 | D.4个 |

(1)当x=-1时:y=a-b+c>0,故(1)正确,
(2)由图象可知:方程ax2+bx+c=0两根:-1<x1<0,1<x2<2,
∴两根之和大于零,故(2)正确;
(3)二次函数图象由对称轴x=-
分开,结合图象可知:当x<-
时,y随x的增大而减小,当x>-
时,y随x的增大而增大,故(3)错误;
(4)由图象可知:-
>0,
∵抛物线开口向上,
∴a>0,
∴b<0,
当x=0时,y=c,结合图象可知:c<0,
∴bc>0,
∴一次函数y=x+bc的图象一定不过第四象限,故(4)正确.
综上:正确的有3个.
故选:C.
(2)由图象可知:方程ax2+bx+c=0两根:-1<x1<0,1<x2<2,
∴两根之和大于零,故(2)正确;
(3)二次函数图象由对称轴x=-
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
(4)由图象可知:-
| b |
| 2a |
∵抛物线开口向上,
∴a>0,
∴b<0,
当x=0时,y=c,结合图象可知:c<0,
∴bc>0,
∴一次函数y=x+bc的图象一定不过第四象限,故(4)正确.
综上:正确的有3个.
故选:C.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目