题目内容
【题目】某游乐场普通门票价格40元/张,为了促销,新推出两种办卡方式:
①白金卡售价200元/张,每次凭卡另收取20元;
②钻石卡售价1000元/张,每次凭卡不再收费.
促销期间普通门票正常出售,两种优惠卡不限次数,设去游乐场玩x次时,所需总费用为y元.
(1)分别写出选择白金卡、普通门票消费时,y与x之间的函数关系式.
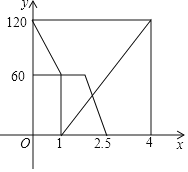
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点B,C的坐标.
(3)请根据图象,直接写出选择哪种消费方式更合算.
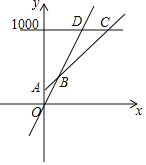
【答案】(1)白金卡:y=20x+200.门票:y=40x;(2)B(10,400),C(40,1000);(3)见解析.
【解析】
(1)根据白金卡售价200元/张,每次凭卡另收取20元,普通门票正常出售,设消费x次时,分别得出所需总费用为y与x之间的关系式即可;
(2)利用函数交点坐标求法分别得出即可;
(3)根据图象解答即可.
解:(1)根据题意可得:白金卡:y=20x+200.
门票:y=40x
(2)将y=40x代入y=200+20x,得40x=200+20x,
解得x=10,
把x=10代入y=40x,得y=400,
所以B(10,400),
把y=1000代入y=200+20x,得1000=200+20x,
解得x=40,
所以C(40,1000);
(3)当0<x<10时,选普通门票;当x=10时,选普通门票和白金卡;
当10<x<40时,选白金卡;
当x=40时,选白金卡和钻石卡;
当x>40时,选钻石卡

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目