题目内容
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() ,
,![]() 上,且
上,且![]() ,
,![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,
,![]()

(1)求证:![]() .
.
(2)判断![]() 的形状,并说明理由.
的形状,并说明理由.
(3)若![]() ,当
,当![]() _______时,
_______时,![]() .请说明理由.
.请说明理由.
【答案】(1)见解析;(2)△ABC是等边三角形,理由见解析;(3)![]() ,理由见解析
,理由见解析
【解析】
(1)根据等边对等角可证∠B=∠C,然后利用SAS即可证出结论;
(2)根据全等三角形的性质可得∠BFD=∠CDE,从而得出∠B=∠1=60°,然后根据等边三角形的判定定理即可得出结论;
(3)作FM⊥BC于M,利用30°所对的直角边是斜边的一半即可求出BM,从而求出BD.
(1)证明:∵AB=AC,
∴∠B=∠C,
在△BDF和△CED中,
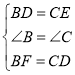 ,
,
∴△BDF≌△CED(SAS);
(2)解:△ABC是等边三角形,理由如下:
由(1)得:△BDF≌△CED,
∴∠BFD=∠CDE,
∵∠CDF=∠B+∠BFD=∠1+∠CDE,
∴∠B=∠1=60°,
∵AB=AC,
∴△ABC是等边三角形
(3)解:当![]() 时,DF⊥BC,理由如下:
时,DF⊥BC,理由如下:
作FM⊥BC于M,如图所示:
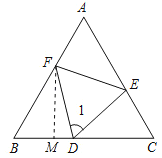
由(2)得:△ABC是等边三角形,
∴∠B=∠C=60°,
∵FM⊥BC,
∴∠BFM=30°,
∴![]() ,
,
∴![]() ,
,
∵![]()
∴M与D重合,
∴![]() 时,DF⊥BC
时,DF⊥BC
故答案为:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】商场销售某种冰箱,该种冰箱每台进价为2500元.已知原销售价为每台2900元时,平均每天能售出8台.若在原销售价的基础上每台降价50元,则平均每天可多售出4台.设每台冰箱的实际售价比原销售价降低了x元.
(1)填表(不需化简):
每天的销售量/台 | 每台销售利润/元 | |
降价前 | 8 | 400 |
降价后 |
(2)商场为使这种冰箱平均每天的销售利润达到5000元,则每台冰箱的实际售价应定为多少元?