Question

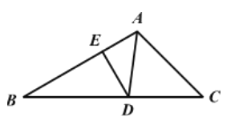
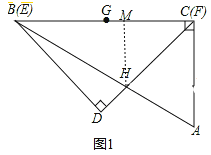
【题目】一副含30°和45°角的三角板ABC和DEF叠合在一起，边BC与EF重合，BC=EF=12cm（如图1），点G为边BC（EF）的中点，边FD与AB相交于点H，此时线段BH的长是____．现将三角板DEF绕点G按顺时针方向旋转（如图2），在∠CGF从0°到60°的变化过程中，点H相应移动的路径长共为_________．（结果保留根号）.

Answer 1

【答案】 12-12 12-18

【解析】解：如图1中，作HM⊥BC于M，设HM=a，则CM=HM=a．

在Rt△ABC中，∠ABC=30°，BC=12，在Rt△BHM中，BH=2HM=2a，BM=a，∵BM+FM=BC，∴ a+a=12，∴a=6﹣6，∴BH=2a=．

如图2中，当DG⊥AB时，易证GH1⊥DF，此时BH1的值最小，易知BH1=BK+KH1=3+3，

∴HH1=BH﹣BH1=9﹣15，当旋转角为60°时，F与H2重合，易知BH2=6，观察图象可知，在∠CGF从0°到60°的变化过程中，点H相应移动的路径长=2HH1+HH2=18﹣30+[6﹣（12﹣12）]= ．故答案为： ， ．