ћвƒњƒЏ»Ё
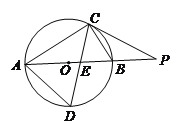
°Њћвƒњ°њ»зЌЉ£ђ‘Џ°чABC÷–£ђ°ѕB£љ45°г£ђBC£љ5£ђЄяAD£љ4£ђЊЎ–ќEFPQµƒ“ї±яQP‘ЏBC±я…ѕ£ђE°ҐFЈ÷±р‘ЏAB°ҐAC…ѕ£ђADљїEF”ЏµгH£Ѓ
£®1£©µ±ЊЎ–ќEFPQќ™’эЈљ–ќ ±£ђ«у’эЈљ–ќµƒ±я≥§£ї
£®2£©…иEF£љx£ђµ±xќ™Їќ÷µ ±£ђЊЎ–ќEFPQµƒ√жїэ„оіу£њ≤Ґ«у≥ц„оіу√жїэ£ї
£®3£©µ±ЊЎ–ќEFPQµƒ√жїэ„оіу ±£ђЄ√ЊЎ–ќEFPQ“‘√њ√л1Єцµ•ќїµƒЋўґ»—Ў…дѕяBC‘»Ћўѕт”“‘Ћґѓ£®µ±ЊЎ–ќµƒґ•µгQµљіпCµг ±Ќ£÷є‘Ћґѓ£©£ђ…и‘Ћґѓ ±Љдќ™t√л£ђЊЎ–ќEFPQ”л°чABC÷Ўµю≤њЈ÷µƒ√жїэќ™S£ђ«уS”лtµƒЇѓ эєЎѕµ љ£ђ≤Ґ–і≥цtµƒ»°÷µЈґќІ£Ѓ

°Њір∞Є°њ£®1£©µ±ЊЎ–ќEFPQќ™’эЈљ–ќ ±£ђ±я≥§ќ™![]() £ї£®2£©µ±x=
£ї£®2£©µ±x=![]() ±£ђЊЎ–ќEFPQµƒ√жїэ„оіу£ђ„оіу√жїэќ™5£ї£®3£©µ±0°№t°№
±£ђЊЎ–ќEFPQµƒ√жїэ„оіу£ђ„оіу√жїэќ™5£ї£®3£©µ±0°№t°№![]() ±£ђS =5-2t2£їµ±
±£ђS =5-2t2£їµ±![]() £Љt£Љ2.5 ±£ђS£љ
£Љt£Љ2.5 ±£ђS£љ![]() -2t£їµ±2.5°№t°№3 ±£ђS£љ2t2-12t+18
-2t£їµ±2.5°№t°№3 ±£ђS£љ2t2-12t+18
°Њљвќц°њ£®1£©”…ћхЉюњ…µ√![]() £ђЉі
£ђЉі![]() £ђЉ∆ЋгЉіњ….
£ђЉ∆ЋгЉіњ….
£®2£©њ…јы”√![]() ”√x±н Њ≥цEH£Ѓ±н Њ≥цЊЎ–ќEFPQµƒ√жїэ£ђјы”√ґюіќЇѓ эњ…«уµ√∆д„оіу÷µ£ї
”√x±н Њ≥цEH£Ѓ±н Њ≥цЊЎ–ќEFPQµƒ√жїэ£ђјы”√ґюіќЇѓ эњ…«уµ√∆д„оіу÷µ£ї
£®3£©Ј÷0°№t°№![]() £ђ
£ђ![]() £ђ2.5°№t°№3»э÷÷«йњцљш––ћ÷¬џЉіњ….
£ђ2.5°№t°№3»э÷÷«йњцљш––ћ÷¬џЉіњ….
(1)°яЋƒ±я–ќEFPQќ™ЊЎ–ќ£ђ
°аEF°ќBC£ђ
![]() £ђ
£ђ
Љі![]() £ђ
£ђ
љвµ√![]()
°аµ±ЊЎ–ќEFPQќ™’эЈљ–ќ ±£ђ±я≥§ќ™![]() .
.
Љіµ±xќ™![]() ±£ђЊЎ–ќEFPQќ™’эЈљ–ќ£ї
±£ђЊЎ–ќEFPQќ™’эЈљ–ќ£ї
£®2£©°я°ѕB=45°г£ђ
°а![]() £ђ
£ђ
°а![]()
°яEF°ќBC£ђ
°а°чAEH°„°чABD£ђ°а![]() £ђ
£ђ
°яEF°ќBC£ђ°а°чAFH°„°чACD£ђ°а![]() £ђ
£ђ
°а![]() £ђЉі
£ђЉі![]() £ђ°а
£ђ°а![]() £ђ
£ђ
“—÷™EF=x£ђ‘тEH=![]() £Ѓ
£Ѓ
°я°ѕB=45°г£ђ
°а![]() =4©Б
=4©Б![]() £Ѓ
£Ѓ
SЊЎ–ќEFPQ![]()
°аµ±x=![]() ±£ђЊЎ–ќEFPQµƒ√жїэ„оіу£ђ„оіу√жїэќ™5£Ѓ
±£ђЊЎ–ќEFPQµƒ√жїэ„оіу£ђ„оіу√жїэќ™5£Ѓ
£®3£©»зЌЉҐў£ђµ±0°№t°№![]() ±
±

…иEFљїAC”ЏMµг£ђFPљїAC”ЏNµг£ђ
°я°чMNF°„°чCAD£ђ
°а![]() £ђ
£ђ
Љі![]() £ђ
£ђ
°аFN=4t £ђ
°аS=5-![]() t°§4t£ђ
t°§4t£ђ
=5-2t2
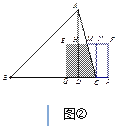
»зЌЉҐЏ£ђµ±![]() ±
±
…иEFљїAC”ЏMµг£ђєэC„чCN°ЌEF”ЏNµг£ђ
°я°чCNM°„°чADC
°а![]() £ђ
£ђ
Љі![]() £ђ
£ђ
°аMN=![]() £ђ
£ђ
°аFN=t-![]() £ђ
£ђ
°аS=5-![]() £®t-
£®t-![]() +t£©£ђ
+t£©£ђ
=![]() -2t £ђ
-2t £ђ
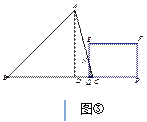
»зЌЉҐџ£ђµ±2.5°№t°№3 ±
…иEQљїAC”ЏNµг£ђ
°я°чCQN°„°чCDA
°а![]() £ђ
£ђ
![]() £ђ
£ђ
°аNQ=12-4t£ђ
°аS=![]() (3-t)(12-4t)
(3-t)(12-4t)
=2t2-12t+18