题目内容
【题目】在正方形ABCD中,
(1)如图1,若点E,F分别在边BC,CD上,AE,BF交于点O,且∠AOF=90°.求证:AE=BF.
(2)如图2,将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G.若DC=5,CM=2,求EF的长.
【答案】
(1)
解:如图1,
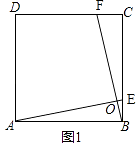
∵四边形ABCD是正方形,
∴AB=BC,∠ABE=∠BCF=90°,
∵∠AOF=90°,
∴∠BAE+∠OBA=90°,
又∵∠FBC+∠OBA=90°,
∴∠BAE=∠CBF,
在△ABE和△BCF中
∵ 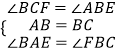 ,
,
∴△ABE≌△BCF(ASA).
∴AE=BF.
(2)
解:由折叠的性质得EF⊥AM,
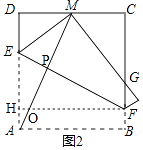
过点F作FH⊥AD于H,交AM于O,
则∠ADM=∠FHE=90°,
∴∠HAO+∠AOH=90°、∠HAO+∠AMD=90°,
∴∠POF=∠AOH=∠AMD,
又∵EF⊥AM,
∴∠POF+∠OFP=90°、∠HFE+∠FEH=90°,
∴∠POF=∠FEH,
∴∠FEH=∠AMD,
∵四边形ABCD是正方形,
∴AD=CD=FH=5,
在△ADM和△FHE中,
∵ 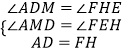 ,
,
∴△ADM≌△FHE(AAS),
∴EF=AM= ![]() =
= ![]() =
= ![]()
【解析】(1)由正方形的性质得AB=BC、∠ABE=∠BCF=90°,由∠AOF=90°得∠BAE=∠CBF,再证△ABE≌△BCF即可得;(2)作FH⊥AD,结合折叠性质:EF⊥AM,证∠POF=∠AOH=∠AMD=∠FEH,再证△ADM≌△FHE得EF=AM= ![]() .
.

【题目】6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频数分布直方图如下:

(1)直接写出a的值,并补全频数分布直方图.
分组 | 频数 | 频率 |
49.5~59.5 | 0.08 | |
59.5~69.5 | 0.12 | |
69.5~79.5 | 20 | |
79.5~89.5 | 32 | |
89.5~100.5 | a |
(2)若成绩在80分以上(含80分)为优秀,求这次参赛的学生中成绩为优秀的约为多少人?
(3)若这组被抽查的学生成绩的中位数是80分,请直接写出被抽查的学生中得分为80分的至少有多少人?
