题目内容
在一个三角形中,有一边边长为16,这条边上的中线和高线长度分别为10和9,求三角形中此边所对的角的正切值.
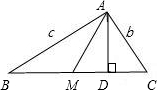
如图,在△ABC中,设AB=c,AC=b,BC=16,中线AM和高线AD分别为10和9,∠BAC=α,∠AMC=θ,从而∠AMB=180°-θ,由题意得,
,解得bccosα=36,
又由
bcsinα=
×9×16,得bcsinα=144,
故tanα=
=4.
|
又由
| 1 |
| 2 |
| 1 |
| 2 |
故tanα=
| sinα |
| cosα |


练习册系列答案
相关题目

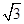 cm,则AB与平面P的夹角为
cm,则AB与平面P的夹角为 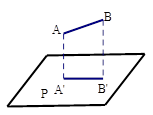
 中,
中, 则
则 的值为
的值为
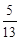


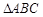 中,
中,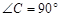 ,
,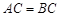 ,若点
,若点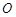 是
是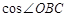 =_______
=_______ 的速度向B移动,到达B后停止;t(秒)为E点移动的时间.
的速度向B移动,到达B后停止;t(秒)为E点移动的时间.