题目内容
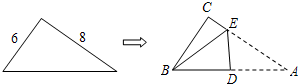
直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是( )

A.
| B.
| C.
| D.
|
根据题意,BE=AE.设CE=x,则BE=AE=8-x.
在Rt△BCE中,根据勾股定理得:BE2=BC2+CE2,即(8-x)2=62+x2
解得x=
,
∴tan∠CBE=
=
=
.
故选C.
在Rt△BCE中,根据勾股定理得:BE2=BC2+CE2,即(8-x)2=62+x2
解得x=
| 7 |
| 4 |
∴tan∠CBE=
| CE |
| CB |
| ||
| 6 |
| 7 |
| 24 |
故选C.

练习册系列答案
相关题目