题目内容
已知二次函数y=x2-(m2-4m+| 5 |
| 2 |
| 9 |
| 2 |
(1)若△ABC为Rt△,求m的值;
(2)在△ABC中;若AC=BC,求∠ACB的正弦值;
(3)设△ABC的面积为S,求当m为何值时,S有最小值,并求这个最小值.
分析:(1)令抛物线的解析式中y=0,可求出A、B点的坐标;若△ABC为直角三角形,则∠ACB必为直角,根据射影定理,即可求出m的值;
(2)若AC=BC,则O是AB的中点,由此可确定A、B、C的坐标,进而可根据△ABC面积的不同表示方法求出∠ACB的正弦值;
(3)根据A、B、C三点的坐标,可求出关于S、m的函数关系式,根据所得函数的性质即可求出S的最小值.
(2)若AC=BC,则O是AB的中点,由此可确定A、B、C的坐标,进而可根据△ABC面积的不同表示方法求出∠ACB的正弦值;
(3)根据A、B、C三点的坐标,可求出关于S、m的函数关系式,根据所得函数的性质即可求出S的最小值.
解答:解:设k=m2-4m+
,
则k+2=m2-4m+
,k=(m-2)2-
≥-
,
∴y=x2-kx-2(k+2)=(x+2)(x-k-2),
∴抛物线与x轴的两个交点为(-2,0),(k+2,0),
∵k≥-
,k+2≥
>-2,
∴A(-2,0),B(k+2,0),C(0,-2k-4),
∴OA=2,OB=k+2,OC=2k+4,
(1)由于A、B位于原点两侧,若△ABC为Rt△,且OC⊥AB,则有:
OC2=OA•OB,
即:(2k+4)2=2(k+2),
解得k=-
,
∴m2-4m+
=-
,
即m2-4m+4=0,
解得m=2;
(2)若AC=BC,则△ABC是等腰三角形,由于OC⊥AB,则OA=OB,
抛物线的对称轴与y轴重合,此时k=0,B(2,0),C(0,-4),
∴AC2=BC2=20;
∵S△ABC=
AC•sinACB•BC=
AB•OC,
∴sin∠ACB=
=
=
;
(3)∵S=
AB•OC=
(k+4)(2k+4)=(k+4)(k+2)=k2+6k+8=(k+3)2-1,
∴当k>-3时,S随k的增大而增大,
由于k≥-
,∴当k=-
时,S取最小值,
∴m2-4m+
=-
,即m=2时,S取最小值,且最小值为S=(3-
)2-1=
.
| 5 |
| 2 |
则k+2=m2-4m+
| 9 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴y=x2-kx-2(k+2)=(x+2)(x-k-2),
∴抛物线与x轴的两个交点为(-2,0),(k+2,0),
∵k≥-
| 3 |
| 2 |
| 1 |
| 2 |
∴A(-2,0),B(k+2,0),C(0,-2k-4),
∴OA=2,OB=k+2,OC=2k+4,
(1)由于A、B位于原点两侧,若△ABC为Rt△,且OC⊥AB,则有:
OC2=OA•OB,
即:(2k+4)2=2(k+2),
解得k=-
| 3 |
| 2 |
∴m2-4m+
| 5 |
| 2 |
| 3 |
| 2 |
即m2-4m+4=0,
解得m=2;
(2)若AC=BC,则△ABC是等腰三角形,由于OC⊥AB,则OA=OB,
抛物线的对称轴与y轴重合,此时k=0,B(2,0),C(0,-4),
∴AC2=BC2=20;
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴sin∠ACB=
| AB•OC |
| AC•BC |
| 16 |
| 20 |
| 4 |
| 5 |
(3)∵S=
| 1 |
| 2 |
| 1 |
| 2 |
∴当k>-3时,S随k的增大而增大,
由于k≥-
| 3 |
| 2 |
| 3 |
| 2 |
∴m2-4m+
| 5 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
点评:此题是典型的二次函数综合题;需要注意的几点是:
①由于m的表达式较大,且含有二次项,若不用k来设m的表达式,本题的计算量将会很大;
②在(2)题中,若不能联想到三角形面积的另一种计算方法:S=
ab•sinC,解题过程将会很复杂;
③在(3)题中,一定要注意k的取值范围,以免造成错解.
①由于m的表达式较大,且含有二次项,若不用k来设m的表达式,本题的计算量将会很大;
②在(2)题中,若不能联想到三角形面积的另一种计算方法:S=
| 1 |
| 2 |
③在(3)题中,一定要注意k的取值范围,以免造成错解.

练习册系列答案
相关题目
已知二次函数y=x2+(2a+1)x+a2-1的最小值为0,则a的值是( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
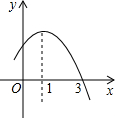 已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为( )
已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为( )| A、x1=1,x2=3 | B、x1=0,x2=3 | C、x1=-1,x2=1 | D、x1=-1,x2=3 |
 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).