Question

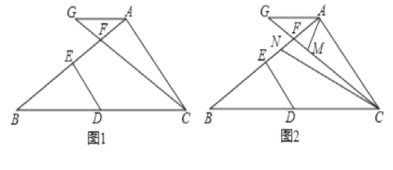
【题目】如图，在Rt△ABC中，∠C=90°，∠A的平分线交BC于D. 过C点作CG⊥AB于G，交AD于E. 过D点作DF⊥AB于F. 下列结论：①∠CED=∠CDE；②S△AEC：S△AEG=AC：AG；③∠ADF=2∠FDB；④CE=DF.其中正确的结论有（ ）

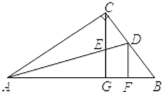
A.1个B.2个C.3个D.4个

Answer 1

【答案】C

【解析】

由∠C=90°，CG⊥AB，得∠ACE=∠B，再由外角的性质，得∠CED=∠CDE，得CE=CD；根据角平分线的性质，得CD=DF，则S△AEC：S△AEG=AC：AG；得CE=DF，从而得出答案．

∵∠ACE+∠BCG=90°，∠B+∠BCG=90°

∴∠ACE=∠B

∵∠CED=∠CAE+∠ACE，∠CDE=∠B+∠DA

∴∠CED=∠CDE，故①正确；

∴CE=CD

又AE平分∠CAB

∴CD=DF

∴CE=DF，故④正确；

过E作EH垂直于AC由角平线性质得EH=EG

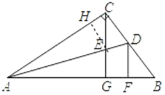
可得S△AEC：S△AEG=ACEH：AGEG=AC：AG；故②正确；

无法证明∠ADF=2∠FDB，故④错误．

∴正确的结论有3个.

故选：C．