题目内容
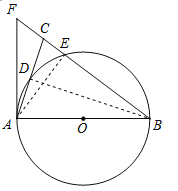
【题目】如图．在△ABC中，BA=BC，以AB为直径的⊙O分别交AC，BC于点D、E，BC的延长线与⊙O的切线AF交于点F．
（1）求证：∠ABC=2∠CAF；
（2）已知AC=2
，EB=4CE，求⊙O的直径．
【答案】（1）答案见解析；（2）10．
【解析】试题分析：（1）首先连接BD，由AB为直径，可得∠ADB=90°，又由AF是⊙O的切线，易证得∠CAF=∠ABD．然后由BA=BC，证得：∠ABC=2∠CAF；
（2）首先连接AE，设CE=x，由勾股定理可得方程：（2
）2=x2+（3x）2求得答案．
试题解析：（1）证明：如图，连接BD．
∵AB为⊙O的直径，∴∠ADB=90°，∴∠DAB+∠ABD=90°．
∵AF是⊙O的切线，∴∠FAB=90°，即∠DAB+∠CAF=90°，∴∠CAF=∠ABD．
∵BA=BC，∠ADB=90°，∴∠ABC=2∠ABD，∴∠ABC=2∠CAF．
（2）如图，连接AE，∴∠AEB=90°，设CE=x．∵CE：EB=1：4，∴EB=4x，BA=BC=5x，AE=3x．在Rt△ACE中，AC2=CE2+AE2，即（2
）2=x2+（3x）2，∴x=2，∴BA=10．
【题目】某天上午出租车司机小张在东西走向的大街上营运，如果规定向东为正，向西为负，他这天上午所接送六位乘客的行驶里程（单位：km）如下表：（等待乘客时，空车里程忽略不计）
乘客顺序 | 第一位 | 第二位 | 第三位 | 第四位 | 第五位 | 第六位 |
行驶里程 | -2 | +8 | -1 | +1 | -9 | -2 |
（1）将最后一位乘客送到目的地时，小张在出发地什么位置？
（2）若汽车耗油量为0.06
,这天上午小张接送乘客，出租车共耗油多少升？
（3）若出租车起步价为5元，起步里程为3km（包括3km），超过部分1.2元/km，问小张这天上午共收车费多少元？
