题目内容
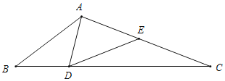
【题目】在△ABC中,∠B=30°,点D在BC边上,点E在AC边上,AD=BD,DE=CE,若△ADE为等腰三角形,则∠C的度数为_____°.
【答案】20或40.
【解析】
先根据三角形外角的性质,得出∠ADC=60°,则设∠C=∠EDC=α,进而得到∠ADE=60°α,∠AED=2α,∠DAE=120°α,最后根据△ADE为等腰三角形,进行分类讨论即可.
解:如图所示,∵AD=BD,∠B=30°,
∴∠BAD=30°,
∴∠ADC=60°,
∵DE=CE,
∴可设∠C=∠EDC=α,则∠ADE=60°﹣α,∠AED=2α,
根据三角形内角和定理可得,∠DAE=180°-(60°﹣α)-(2α)=120°﹣α,
分三种情况:
①当AE=AD时,则∠ADE=∠AED,即60°﹣α=2α,
解得α=20°;
②当DA=DE时,则∠DAE=∠AED,即120°﹣α=2α,
解得α=40°;
③当EA=ED时,则∠DAE=∠ADE,即120°﹣α=60°﹣α,方程无解,
综上所述,∠C的度数为20°或40°,
故答案为:20或40.

练习册系列答案
相关题目





