题目内容
【题目】有两个内角分别是它们对角的一半的四边形叫做半对角四边形
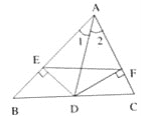
(1)如图1,在半对角四边形ABCD中,∠B=![]() ∠D,∠C=
∠D,∠C=![]() ∠A,求∠B与∠C的度数之和;
∠A,求∠B与∠C的度数之和;
(2)如图2,锐角△ABC内接于⊙O,若边AB上存在一点D,使得BD=BO,∠OBA的平分线交OA于点E,连结DE并延长交AC于点F,∠AFE=2∠EAF.求证:四边形DBCF是半对角四边形;
(3)如图3,在(2)的条件下,过点D作DG⊥OB于点H,交BC于点G,当DH=BG=2时,求⊙O的直径.

【答案】(1) ∠B与∠C的度数和为120°;(2)详见解析;(3)8.
【解析】
根据题意得出∠B=![]() ∠D,∠C=
∠D,∠C=![]() ∠A,代入∠A+∠B+∠C+∠D=360°求出即可;
∠A,代入∠A+∠B+∠C+∠D=360°求出即可;
求出△BED≌△BEO ,根据全等得出∠BDE=∠BOE ,连接OC,设∠EAF=α,则∠AFE=2∠EAF=2α,求出∠EFC=180°-∠AFE=180°-2α,∠AOC=180°-2α,即可得出等答案;
过点O作OM⊥BC,再由角与角之间关系得出边与边之间关系,进而得出解.
(1)在半对角四边形ABCD中,∠B=![]() ∠D,∠C=
∠D,∠C=![]() ∠A,∵∠A+∠B+∠C+∠D=360°,∴3∠B+3∠C=360°,∴∠B+∠C=120°,即∠B与∠C的度数和为120°;
∠A,∵∠A+∠B+∠C+∠D=360°,∴3∠B+3∠C=360°,∴∠B+∠C=120°,即∠B与∠C的度数和为120°;
(2)证明:∵在△BED和△BEO中BD=BO,∠EBD=∠EBO,BE=BE∴△BED≌△BEO,∴∠BDE=∠BOE,∵∠BCF=![]() ∠BOE,∴∠BCF=
∠BOE,∴∠BCF=![]() ∠BDE,连接OC,设∠EAF=α,则∠AFE=2∠EAF=2α,∴∠EFC=180°-∠AFE=180°-2α,∵OA=OC,∴∠OAC=∠OCA=α,∴∠AOC=180°-∠OAC-∠OCA=180°-2α,∴∠ABC=
∠BDE,连接OC,设∠EAF=α,则∠AFE=2∠EAF=2α,∴∠EFC=180°-∠AFE=180°-2α,∵OA=OC,∴∠OAC=∠OCA=α,∴∠AOC=180°-∠OAC-∠OCA=180°-2α,∴∠ABC=![]() ∠AOC=
∠AOC=![]() ∠EFC,∴四边形DBCF是半对角四边形;
∠EFC,∴四边形DBCF是半对角四边形;
(3)解:过点O作OM⊥BC于M,∵四边形DBCF是半对角四边形,∴∠ABC+∠ACB=120°,∴∠BAC=60°,∴∠BOC=2∠BAC=120°,∵OB=OC,∴∠OBC=∠OCB=30°,∴BC=2BM=![]() BO=
BO=![]() BD,∵DG⊥OB,∠DBO=30°,∵DH=BG=2时,BD=4,直径=8.
BD,∵DG⊥OB,∠DBO=30°,∵DH=BG=2时,BD=4,直径=8.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案【题目】二次函数![]() (a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
给出了结论:
(1)二次函数![]() 有最小值,最小值为﹣3;
有最小值,最小值为﹣3;
(2)当![]() 时,y<0;
时,y<0;
(3)二次函数![]() 的图象与x轴有两个交点,且它们分别在y轴两侧.
的图象与x轴有两个交点,且它们分别在y轴两侧.
则其中正确结论的个数是
A. 3 B. 2 C. 1 D. 0