题目内容
【题目】如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.
(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由. 
【答案】
(1)
解:①如图,连接BD,
∵AB是直径,
∴∠ACB=∠ADB=90°,
在Rt△ABC中,
AC= ![]() =
= ![]() =5
=5 ![]() (cm),
(cm),
②∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴ ![]() ,
,
∴AD=BD,
∴Rt△ABD是直角等腰三角形,
∴AD= ![]() AB=
AB= ![]() ×10=5
×10=5 ![]() cm;
cm;
(2)
解:直线PC与⊙O相切,
理由:连接OC,
∵OC=OA,
∴∠CAO=∠OCA,
∵PC=PE,
∴∠PCE=∠PEC,
∵∠PEC=∠CAE+∠ACE,
∵CD平分∠ACB,
∴∠ACE=∠ECB,
∴∠PCB=∠CAO=∠ACO,
∵∠ACB=90°,
∴∠OCP=∠OCB+∠PCB=∠ACO+∠OCB=∠ACB=90°,
即OC⊥PC,
∴直线PC与⊙O相切.
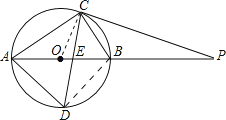
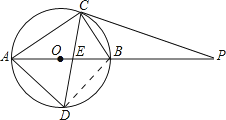
【解析】(1)连接BD,先求出AC,在Rt△ABC中,运用勾股定理求AC,②由CD平分∠ACB,得出AD=BD,所以Rt△ABD是直角等腰三角形,求出AD,(2)连接OC,由角的关系求出∠PCB=∠ACO,可得到∠OCP=90°,所以直线PC与⊙O相切.
【考点精析】本题主要考查了勾股定理的概念和圆周角定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.

【题目】某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
运动项目 | 频数(人数) | 频率 |
篮球 | 30 | 0.25 |
羽毛球 | m | 0.20 |
乒乓球 | 36 | n |
跳绳 | 18 | 0.15 |
其它 | 12 | 0.10 |
请根据以上图表信息解答下列问题:
(1)频数分布表中的m= , n=;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为 °;
(3)从选择“篮球”选项的30名学生中,随机抽取3名学生作为代表进行投篮测试,则其中某位学生被选中的概率是 




