题目内容
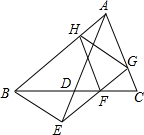如图，AD是△ABC中线，F是DC上一点，过F作AB、AC平行线交AC、AB分别于G、H，GF与AD延长线交于E．求证：GH=BE．
证明：∵GE∥AB，BD=DC，
∴△CFG∽△CBA，△EFD∽△ABD，
∴
①，
②
①+②得，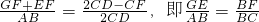
，
∵FH∥AC，
∴△BHF∽△BAC，
∴
∴
，
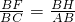∴GE=BH，
∵GE∥AB
∴四边形BEGH为平行四边形，
∴BE=GH．
分析：根据条件求出△CFG∽△CBA，△EFD∽△ABD，然后根据相似三角形的对应边成比例求出线段相等，然后判断出四边形BEGH为平行四边形，从而得解．
点评：本题考查了全等三角形的判定定理和性质定理，然后根据判定和性质求出解．
∴△CFG∽△CBA，△EFD∽△ABD，
∴
①，②①+②得，
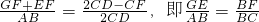，∵FH∥AC，
∴△BHF∽△BAC，
∴
∴，∴GE=BH，
∵GE∥AB
∴四边形BEGH为平行四边形，
∴BE=GH．
分析：根据条件求出△CFG∽△CBA，△EFD∽△ABD，然后根据相似三角形的对应边成比例求出线段相等，然后判断出四边形BEGH为平行四边形，从而得解．
点评：本题考查了全等三角形的判定定理和性质定理，然后根据判定和性质求出解．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
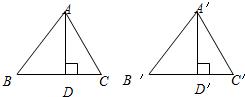
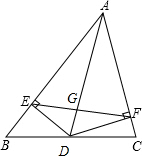如图，AD是△ABC是角平分线，DE⊥AB于点E，DF⊥AC于点F，连接EF交AD于点G，则AD与EF的位置关系是
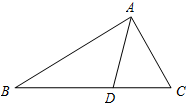16、已知：如图，AD是△ABC的角平分线，且 AB：AC=3：2，则△ABD与△ACD的面积之比为
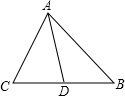如图，AD是△ABC的边BC上的中线，已知AB=5cm，AC=3cm．
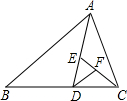如图，AD是△ABC的中线，CE是△ACD的中线，DF是△CDE的中线，如果△DEF的面积是2，那么△ABC的面积为（ ）