��Ŀ����
����Ŀ���Ķ�������ϲ�����й����⣺
����֪����|x|=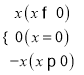 ���������ǿ�������һ�����������о���ֵ�Ĵ���ʽ���������ǿ�������һ�����������о���ֵ�Ĵ���ʽ���绯�����ʽ|x+1|+|x��2|ʱ������x+1=0��x��2=0���ֱ����x=��1��x=2���Ʃ�1��2�ֱ�Ϊ|x+1|��|x��2|�����ֵ������ʵ����Χ�ڣ����ֵx=��1�ͣ�x=2�ɽ�ȫ��ʵ���ֳɲ��ظ��Ҳ���©������3�������
���������ǿ�������һ�����������о���ֵ�Ĵ���ʽ���������ǿ�������һ�����������о���ֵ�Ĵ���ʽ���绯�����ʽ|x+1|+|x��2|ʱ������x+1=0��x��2=0���ֱ����x=��1��x=2���Ʃ�1��2�ֱ�Ϊ|x+1|��|x��2|�����ֵ������ʵ����Χ�ڣ����ֵx=��1�ͣ�x=2�ɽ�ȫ��ʵ���ֳɲ��ظ��Ҳ���©������3�������
��x����1���ک�1��x��2����x��2��
�Ӷ��������ʽ|x+1|+|x��2|�ɷ�����3�������
����x����1ʱ��ԭʽ=����x+1������x��2��=��2x+1��
������1��x��2ʱ��ԭʽ=x+1����x��2��=3��
����x��2ʱ��ԭʽ=x+1+x��2=2x��1���������ۣ�ԭʽ=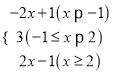 ��
��
ͨ�������Ķ����������������⣺
��1���������ʽ|x+2|+|x��4|��
��2����|x��1|��4|x+1|�����ֵ��
���𰸡���1����x����2ʱ����2x+2������2��x��4ʱ�� 6����x��4ʱ��2x��2����2��2��
�������������������1����Ϊx<-2��-2��x<4��x��4����������ɣ�
��2����x<-1��-1��x��1��x>1�ֱ��x��ȡֵ��Χȷ������ʽֵ�ķ�Χ���Ӷ��������ʽ�����ֵ��
�⣺��1����x����2ʱ��|x+2|+|x��4|=��x��2+4��x=��2x+2��
����2��x��4ʱ��|x+2|+|x��4|=x+2+4��x=6��
��x��4ʱ��|x+2|+|x��4|=x+2+x��4=2x��2��
��2����x����1ʱ��ԭʽ=3x+5��2��
����1��x��1ʱ��ԭʽ=��5x��3����8�ܩ�5x��3��2��
��x��1ʱ��ԭʽ=��3x��5����8��
��|x��1|��4|x+1|�����ֵΪ2��

 Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�